Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A. y = 1 sin 3 x
B. y = sin x + π 4
C. y = 2 cos x - π 4
D. y = sin 2 x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)

a) Tập giá trị của hàm số \(y = \cot x\)là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Hàm số \(y = \cot x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) song song với trục hoành sang phải theo đoạn có độ dài \(\pi \), ta nhận được \(y = \cot x\) trên khoảng \(\left( {\pi ;2\pi } \right)\)
Hàm số \(y = \cot x\) có tuần hoàn
d) Hàm số \(y = \cot x\)nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right),k \in Z\)

Đáp án A
Phương pháp: Tham số hóa điểm thuộc đồ thị hàm số (C).
Lấy điểm đối xứng với điểm đó qua O (Điểm (a;) đối xứng với điểm (-a;-b)qua gốc tọa độ O).
Cho điểm đối xứng vừa xác định thuộc (C).
Cách giải:
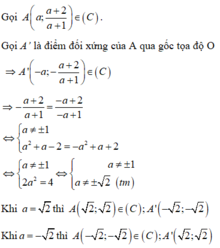
Chú ý và sai lầm : Có thể thử trực tiếp từng đáp án và suy ra kết quả.

a) Tập giá trị của hàm số \(y = \tan x\) là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Như vậy, hàm số \(y = \tan x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)
Như vậy, hàm số \(y = \tan x\) có tuần hoàn
d) Hàm số \(y = \tan x\)đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\) với \(k \in Z\)

a: 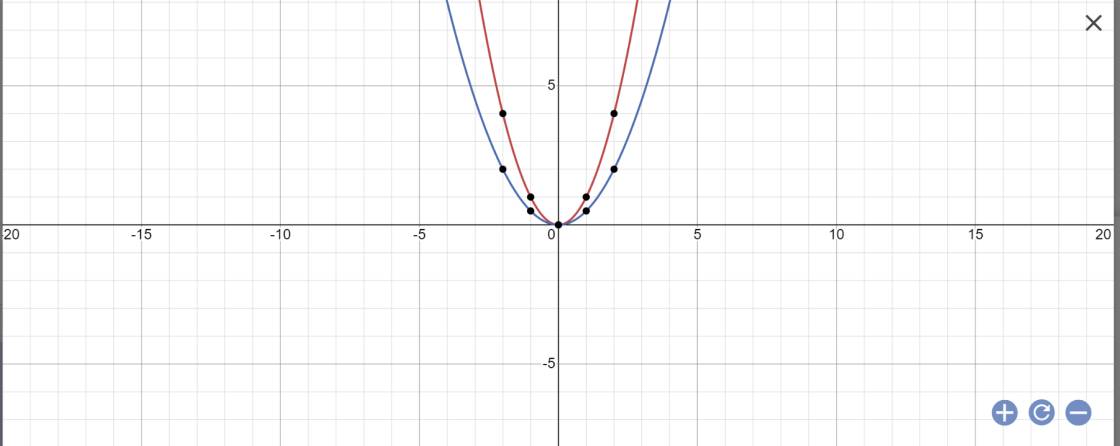
b: Khi x=2 thì y=1/2*2^2=2
=>A(2;2)
Khi x=2 thì y=2^2=4
=>B(2;4)
c: Tọa độ A' là:
\(\left\{{}\begin{matrix}x_{A'}=-x_A=-2\\y_{A'}=y_A=2\end{matrix}\right.\)
Vì f(-2)=1/2*(-2)^2=2
nên A' thuộc (P1)
Tọa độ B' là:
\(\left\{{}\begin{matrix}x_{B'}=-x_B=-2\\y_{B'}=y_B=4\end{matrix}\right.\)
Vì f1(-2)=(-2)^2=4
nên B' thuộc y=x^2
Đáp án A