Cho khối lập phương ABCDA’B’C’D’. Đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A’C’ là :
A. AA’
B. BB'
C. DA’
D. DD’
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
20 tháng 7 2018
tham khảo Câu hỏi của Nữ hoàng sến súa là ta - Toán lớp 8 - Học toán với OnlineMath
CM
23 tháng 5 2018
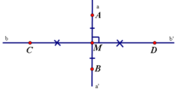
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
CM
6 tháng 8 2019
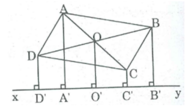
Gọi O là giao điểm của AC và BD
⇒ OA = OC, OB = OD (tính chất hình bình hành)
Kẻ OO' ⊥ xy
AA' ⊥ xy (gt)
CC' ⊥ xy (gt)
Suy ra: AA' // OO' // CC'
Tứ giác ACC'A' là hình thang có:
OA = OC (chứng minh trên)
OO' // AA' nên OO' là đường trung bình của hình thang ACC'A'.
⇒ OO' = (AA' + CC') / 2 (t/chất đường trung bình của hình thang) (1)
BB' ⊥ xy
DD' ⊥ xy (gt)
OO' ⊥ xy (gt)
Suy ra: BB'// OO' // DD'
Tứ giác BDD'B' là hình thang có:
OB = OD (Chứng minh trên)
OO' // BB' nên OO' là đường trung bình của hình thang BDD'B'.
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung bình của hình thang) (2)
Từ (1) và (2) => AA' + CC' = BB + DD'
CM
3 tháng 9 2017
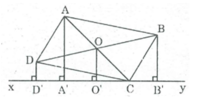
Gọi O là giao điểm của hai đường chéo AC và BD.
Kẻ OO' ⊥ xy
Ta có: BB' ⊥ xy (gt)
DD' ⊥ xy (gt)
Suy ra: BB // OO' // DD'
Tứ giác BB'D'D là hình thang .
OB = OD (t/chất hình bình hành)
Nên O'B' = O'D'
Do đó OO' là đường trung bình của hình thang BB'D'D
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)
AA' ⊥ xy (gt)
OO' ⊥ xy (theo cách vẽ)
Suy ra: AA' // OO'
Trong ∆ ACA' tacó: OA = OC (tính chất hình bình hành)
OO' // AA' nên OO' là đường trung bình của ∆ ACA'
⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)
⇒ AA' = 2OO' (2)
Tử (1) và (2) suy ra: AA' = BB' + DD'
CM
6 tháng 12 2017
a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.
5 tháng 11 2014
(hình bạn tự vẽ nha)CM:
- gọi giao điểm của hai đường chéo là O
- mà tứ giác ABCD là hình bình hành(gt)
- =>\(OA=OC=\frac{1}{2}ACvàOD=OB=\frac{1}{2}BD\)
- kẻ OO' vuông góc với d
- ta có:OO',AA',BB',CC',DD' vuông góc với d nên OO',AA',BB',CC',DD' song song với nhau
cm OO' là đường trung bình của hình thang BB'D'D=>\(OO'=\frac{BB'+DD'}{2}\left(1\right)\)
- chứng minh OO' là đường trung bình của hình thang AA'C'C=>\(OO'=\frac{AA'+CC'}{2}\left(2\right)\)
- từ (1) và (2)=>\(\frac{AA'+CC'}{2}=\frac{BB'+DD'}{2}\Rightarrow AA'+CC'=BB'+D'D\)
TK
25 tháng 9 2017
Gọi O la giao điểm hai đường chéo hình bình hành
Từ O kẻ OO' vông góc với d tại O'
Ta có O' là trg điểm của A'O (do cùng vuông góc và song song với D' trên duog thẳng d )
suy ra OO'là dg trg bình cua tam giac AAC
suy ra AA' = 2 OO'(1)
Ta có DD' song song BB' ( do cùng vuông óc với d)
suy ra DD' ,BB' là hình thang
Ta có
OO' song song DD' song song BB' (cùng vuông góc d)(a)
Và O là trug điểm DB(b(
Từ (a) và(b) suy ra O là trung điểm D'B'
suy ra OO là dg2 trung bình của bình thang DD' BB'
suy ra OO' là dg trug bình của hình thang DD' BB'
suy ra D'B' =2OO' (2)
Từ (1) và (2) suy ra AA' =BB' +DD'
nhớ cho mình nha
Ta có: A A ' ⊥ A D tại A; A A ' ⊥ A ' C ' tại A’
Do đó đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A’C’ là AA’.
Đáp án A