Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và B A D ^ = B A A ' ^ = D A A ' ^ = 60 ° . Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’).
A. a 5 5
B. a 6 3
C. a 10 5
D. a 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương án A sai vì tam giác ACB’ có ba cạnh bằng a
Phương án C sai vì tam giác CB’D’ có ba cạnh a, a√3,a√3 nên không thể vuông tại B’
Phương án D sai vì góc giữa đường thẳng B’C và AA’ bằng 0 o
Phương án B đúng vì:
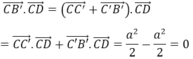
Đáp án B

Phương án A, B và D đều sai
Phương án C đúng vì tam giác CB’D’ có ba cạnh bằng a, a√3,a√3 nên không thể vuông tại B’
Đáp án C

Đáp án C
Diện tích đáy là: S A B C D = a 2 sin 120 ∘ = a 2 3 2 .
Thể tích khối lăng trụ đứng là : V = A A ' . S A B C D = a . a 2 3 2 = a 3 3 2
+ Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD
Ta có: A’B = A’D (đường chéo các hình thoi) ⇒ Tam giác A’BD cân tại A’ có O là trung điểm của BD ⇒ A’O ⊥ BD.
+ Hạ A’H ⊥ AC, H ∈ AC
Ta có B D ⊥ A C B D ⊥ A ' O ⇒ B D ⊥ A O A ' ⇒ A’H ⊥ BD
Do đó: A’H ⊥ (ABCD)
Vì (ABCD) // (A’B’C’D’) nên A’H chính là khoảng cách giữa hai mặt đáy.
+ Tính A’H
Ta có: AC = A D 2 + C D 2 − 2. A D . C D . cos 120 ° = a 3 ⇒ AO = a 3 2
Theo giả thiết ⇒ hình chóp A’.ABD là hình chóp đều, nên ta có:
AH = 2/3 AO = a 3 3
A’H = A ' A 2 − A H 2 = a 2 − a 2 3 = a 6 3
Vậy khoảng cách giữa hai đáy (ABCD) và (A’B’C’D’) là a 6 3 .
Đáp án B