Trong mp Oxy, cho đường thẳng (d): 2018x + 2019y – 1 =0 và vectơ u → 2019 ; m . Tìm m để phép tịnh tiến theo vectơ u → biến (d) thành chính nó
A.–2018
B. –2019
C. 2018
D. 2019
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phép tịnh tiến biến(d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương v → của (d) : v → ( 2019 ; − 2018 ) = k u → = 0 ; k m =>m = 0
=>có một giá trị m = 0 để biến (d) thành chính nó

Đáp án B
Phép tịnh tiến biến (d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương của (d)
v → ( 2019 ; − 2018 ) = k u → 2 k ; k m =>k 2019 2 => m = − 4046 2019
=>có một giá trị m = − 4046 2019 để biến (d) thành chính nó

Đáp án D
Để biến d thành chính nó, ta tịnh tiến d theo VTCP của nó.

Lời giải:
Đặt mẫu số của $B$ là $M$.
Từ \(2018x^3=2019y^3=2020z^3\)
\(\Rightarrow \sqrt[3]{2018}x=\sqrt[3]{2019}y=\sqrt[3]{2020}z=\frac{\sqrt[3]{2018}}{\frac{1}{x}}=\frac{\sqrt[3]{2019}}{\frac{1}{y}}=\frac{\sqrt[3]{2020}}{\frac{1}{z}}=\frac{\sqrt[3]{2018}+\sqrt[3]{2019}+\sqrt[3]{2020}}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}\)
\(=\frac{\sqrt[3]{2018}+\sqrt[3]{2019}+\sqrt[3]{2020}}{8}=\frac{M}{8}\)
\(\Rightarrow \left\{\begin{matrix} x=\frac{M}{8\sqrt[3]{2018}}\\ y=\frac{M}{8\sqrt[3]{2019}}\\ z=\frac{M}{8\sqrt[3]{2020}}\end{matrix}\right.\Rightarrow \left\{\begin{matrix} 2018x^2=\frac{\sqrt[3]{2018}M^2}{64}\\ 2019y^2=\frac{\sqrt[3]{2019}M^2}{64}\\ 2020z^2=\frac{\sqrt[3]{2020}M^2}{64}\end{matrix}\right.\)
\(\Rightarrow 2018x^2+2019y^2+2020z^2=\frac{M^2(\sqrt[3]{2018}+\sqrt[3]{2019}+\sqrt[3]{2020})}{64}=\frac{M^3}{64}\)
\(\Rightarrow B=\frac{\sqrt[3]{\frac{M^3}{64}}}{M}=\frac{M}{4M}=\frac{1}{4}\)

Đáp án A
Ta có 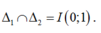
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
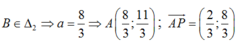
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0

4.
Để phép tịnh tiến theo \(\overrightarrow{v}\) biến d thành chính nó thì \(\overrightarrow{v}\) phải là 1 vecto chỉ phương của d
Khi đó \(\overrightarrow{v}=k\left(1;2\right)\) với k là số thực
5.
Đường tròn tâm \(I\left(2;1\right)\) bán kính \(R=4\)
Phép tịnh tiến theo \(\overrightarrow{v}\) biến đường tròn thành đường tròn tâm I' bán kính R=4
\(I'=T_{\overrightarrow{v}}\left(I\right)\Rightarrow\left\{{}\begin{matrix}x_{I'}=2+1=3\\y_{I'}=3+1=4\end{matrix}\right.\) \(\Rightarrow I'\left(3;4\right)\)
Phương trình đường tròn: \(\left(x-3\right)^2+\left(y-4\right)^2=16\)

Đáp án C
(C) có tâm I(0;2), bán kính 5
Tịnh tiến theo vectơ u → biến I thành I’(2; 0)
=>Phương trình đường tròn (C’): ( x − 2 ) 2 + y 2 = 25
Đáp án A
Phép tịnh tiến biến (d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương của (d)
v → ( 2019 ; − 2018 ) = k u → = 2019 k ; k m => k = 1 m = – 2018
=>có một giá trị m = – 2018 để biến (d) thành chính nó