Cho hình chóp S.ABC có SA, SB, SC tạo với mặt đáy các góc bằng nhau và bằng 60 ⁰ . Biết B C = a , B A C ^ = 45 ° . Tính khoảng cách h từ đỉnh S đến mặt phẳng (ABC).
A. h = a 6 3
B. h = a 6
C. h = a 6
D. h = a 6 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi A’ là hình chiếu của A trên mặt phẳng (P). Khi đó d A ; P = A A ' .
Sử dụng các công thức tính diện tích tam giác ABC
S = 1 2 b c sin A = 1 2 a c sin B = 1 2 a b sin C
Trong đó a, b, c là độ dài các cạnh của tam giác, R là bán kính đường tròn ngoại tiếp tam giác.
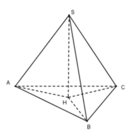
Gọi H là hình chiếu đỉnh S lên mp (ABC) khi đó ta có góc tạo bởi SA, SB, AC với đáy lần lượt là S A H ; S B H ; S C H và S A H = S B H = S C H = 60 °
Dễ dàng chứng minh được Δ S A H = Δ S B H = Δ S C H ⇒ H A = H B = H C ⇒ H là tâm đường tròn ngoại tiếp tam giác Δ A B C .
Đặt S H = h .
Xét tam giác vuông SAH có A H = S H . cot 60 ° = h 3 = R .
Xét tam giác ABC có: S A B C = A B . A C . B C 4 R = A B . A C . a 4 h 3 = 3 a 4 h A B . A C
Mà
S A B C = 1 2 A B . A C . sin B A C = 1 2 2 2 A B . A C = 2 4 A B . A C
⇒ 3 a 4 h = 2 4 ⇔ h = 3 a 2 = a 6 2 .

+)Gọi H là chân đường cao hạ từ A - -> BC
Tam giác AHC vuông tại H nên
AH = √(a² -a²/4) = a√3/2
Diện tích tam giác ABC là S(ABC) = 1/2.AH.BC= 1/2.a²√3/2
(dvdt)
+)Từ S hạ SK ┴ AH , Kết hợp AH ┴ BC ta có SK ┴ (ABC)
Hay SK là đường cao của hình chóp đều SABC
+) Bài cho góc giữa các mặt bên với đáy là 60 độ nên
góc giữa (SH,HK) = 60 độ
Tam giác vuông SKH có SK = HK.tan(60)
Tam giác vuông BKH có HK = a/2.tan(30) = a√3/6
- - > SK = a√3/6.tan(60) = a/2
Vậy V(SABC) =1/3.SK.S(ABC) = 1/3.a/2.1/2.a²√3/2
= a³√3/24 (dvtt)

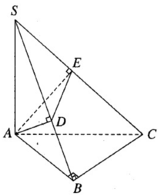
Gọi d là khoảng cách từ E đến mặt phẳng (SAB)
Ta có:
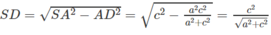
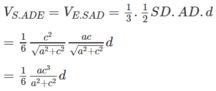
Kết hợp với kết quả trong câu a)
ta suy ra 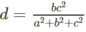

Đáp án B
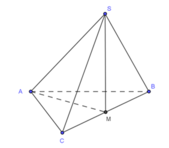
Hình chiếu của S xuống đáy ABC là tâm của đáy tức là M với M là trung điểm của .
Ta có S A , A B C ^ = S A , A M ^ = S A M = 45 0
Vì ABC là tam giác vuông cân nên H cũng là trung điểm của BC vì thế
A M = 1 2 B C = a 2 2
ta có
d S ; A B C = S M = A M . tan S A M = a 2 2 . tan 45 0 = a 2 2

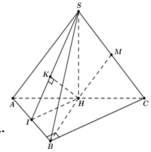
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.