Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
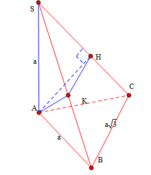
A C = A B 2 + B C 2 = a 2 + 3 a 2 = 2 a
S C = S A 2 + A C 2 = a 2 + 4 a 2 = a 5
S H = S A 2 S C = a 2 a 5 = a 5
S B = S A 2 + A B 2 = a 2 + a 2 = a 2
Δ S H K ~ Δ S B C ⇒ S H S B = S K S C ⇒ S K = S H . S C S B = a . a 5 5 . a 2 = a 2
⇒ V S . A H K V S . A B C = S H S C S K S B = a 5 a 5 a 2 a 2 = 1 10 ⇒ V S . A H K = 1 10 V S . A B C = 1 3 S A . d t A B C = 1 10 . 1 3 a . 1 2 a . a 3 = a 3 3 60

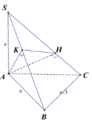
Ta có:
S B = a 2 + b 2 = a 2 A C 2 = a 2 + 3 a 2 = 4 a 2 ⇒ S C = a 2 + 4 a 2 = a 5 S K = S A 2 S B = a 2 a 2 = a 2 S H = S A 2 S C = a 2 a 5 = a 5 V S . A H K V S . A B C = S K . S H S B . S C = 1 2 . 1 5 = 1 10 ⇒ V S . A H K = 1 10 V S . A B C = 1 60 S A . B A . B C = 1 60 3 a 3
Đáp án cần chọn là C

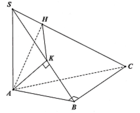
Ta có A K ⊥ S C A K ⊥ α A K ⊥ B C B C ⊥ S A B
Suy ra A K ⊥ S B C ⇒ A K ⊥ S B .
Vì ∆ S A B vuông cân tại A nên K là trung điểm của SB. Ta có
V S . A H K V S . A B C = S A . S K . S H S A . S B . S C = S H 2 S C
Ta có
A V = A B 2 + B C 2 = 2 a S V = A C 2 + S A 2 = a 5 .
Khi đó S H S C = S H . S C S C 2 = S A 2 S C 2 = 1 5
Suy ra V S . A H K V S . A B C = S H 2 S C = 1 10
Mặt khác V S . A B C = 1 3 S A . 1 2 A B . B C = a 3 3 6 Vậy V S . A H K = a 3 3 60
Đáp án C

Đáp án B
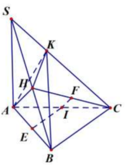
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC. IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
=> IA = IB = IC = IH = IK
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB.
Suy ra bán kính R = 2 π a 3 3

Đáp án B
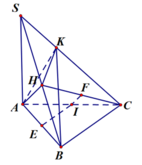
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC.
IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB. Suy ra bán kính R = a 2 2

Đáp án D
Phương pháp giải:
Xác định tâm mặt cầu ngoại tiếp đi qua các đỉnh của khối chóp bằng phương pháp dựng hình, từ đó dựa vào tính toán xác định bán kính – thể tích mặt cầu.
Lời giải:


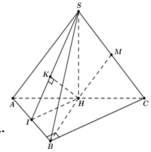
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.


Đáp án C
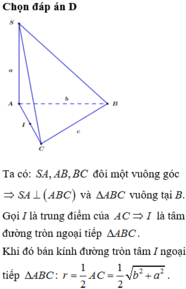
Gọi A’ là hình chiếu của A trên mặt phẳng (P). Khi đó d A ; P = A A ' .
Sử dụng các công thức tính diện tích tam giác ABC
S = 1 2 b c sin A = 1 2 a c sin B = 1 2 a b sin C
Trong đó a, b, c là độ dài các cạnh của tam giác, R là bán kính đường tròn ngoại tiếp tam giác.
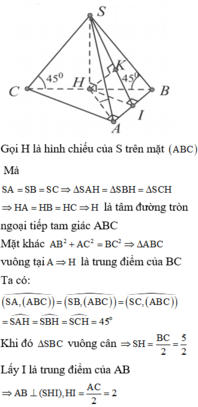
Gọi H là hình chiếu đỉnh S lên mp (ABC) khi đó ta có góc tạo bởi SA, SB, AC với đáy lần lượt là S A H ; S B H ; S C H và S A H = S B H = S C H = 60 °
Dễ dàng chứng minh được Δ S A H = Δ S B H = Δ S C H ⇒ H A = H B = H C ⇒ H là tâm đường tròn ngoại tiếp tam giác Δ A B C .
Đặt S H = h .
Xét tam giác vuông SAH có A H = S H . cot 60 ° = h 3 = R .
Xét tam giác ABC có: S A B C = A B . A C . B C 4 R = A B . A C . a 4 h 3 = 3 a 4 h A B . A C
Mà
S A B C = 1 2 A B . A C . sin B A C = 1 2 2 2 A B . A C = 2 4 A B . A C
⇒ 3 a 4 h = 2 4 ⇔ h = 3 a 2 = a 6 2 .