Cho hàm số f x = 4 x 4 x + 2 và góc α tùy ý. Khi đó giá trị của biểu thức P = f sin 2 α + f cos 2 α bằng
A. 1
B. 2
C. 3
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

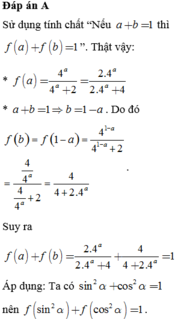

Đáp án A
Sử dụng tính chất “Nếu a + b = 1 thì f a + f b = 1 ”. Thật vậy:
f a = 4 a 4 a + 2 = 2.4 a 2.4 a + 4
a + b = 1 ⇒ b = 1 − a . Do đó f b = f 1 − a = 4 1 − a 4 1 − a + 2 = 4 4 a 4 4 a + 2 = 4 4 + 2.4 a .
Suy ra f a + f b = 2.4 a 2.4 a + 4 + 4 4 + 2.4 a = 1 .
Áp dụng: Ta có sin 2 α + cos 2 α = 1 nên f sin 2 α + f cos 2 α = 1 .

a: \(y=f\left(x^2\right)=sin\left(x^2\right)\)
b: \(y=f\left(g\left(x\right)\right)=f\left(x^2\right)=sinx^2\)

Chọn D.
Xét biểu thức (sin α - cosα ) 2 + (sin α + cosα ) 2 ta có:
(sin α - cosα ) 2 + (sin α + cosα ) 2
= sin 2 α - 2sin α.cosα + cos 2 α + sin 2 α + 2 sin α.cosα + cos 2 α
= 2( sin 2 α + cos 2 α ) =2
⇒ (sin α - cosα ) 2 = 2 - (sin α + cosα ) 2
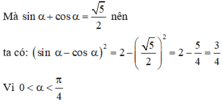
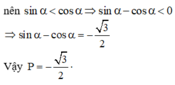

\(sin\left(\text{α}-\dfrac{\Pi}{4}\right)-cos\left(\text{α}-\dfrac{\Pi}{4}\right)\)
\(=sin\text{α}.cos\dfrac{\Pi}{4}-cos\text{α}-sin\dfrac{\Pi}{4}-\left(cos\text{α}.cos\dfrac{\Pi}{4}+sin\text{α}.sin\dfrac{\Pi}{4}\right)\)
\(=sin\text{α}.\dfrac{\sqrt{2}}{2}-\dfrac{1}{3}.\dfrac{\sqrt{2}}{2}-\dfrac{1}{3}.\dfrac{\sqrt{2}}{2}-sin\text{α}.\dfrac{\sqrt{2}}{2}\)
\(=\dfrac{-2\sqrt{2}}{6}\)
\(=\dfrac{-\sqrt{2}}{3}\)