Cho hàm số y = 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?
A. (x1 – x2)2 = 8
B. x1x2 = 2
C. x2 – x1 = 3
D. x12 + x22 = 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phương trình hoành độ giao điểm là:
\(x^2=2x-m+2\)
\(\Leftrightarrow x^2-2x+m-2=0\)
Để hai đồ thị hàm số chỉ có một điểm chung thì Δ=0
\(\Leftrightarrow4-1\cdot\left(m-2\right)=0\)
\(\Leftrightarrow m-2=4\)
hay m=6

Chọn D
![]()
![]()
x 1 , x 2 là hai nghiệm của phương trình y ' = 0
Khi đó, theo định lý Viet, ta có: x 1 + x 2 = 4 .

Chọn C
Ta có: y ' = 2 x 2 - 2 m x - 2 ( 3 m 2 - 1 )
g ( x ) = x 2 - m x - 3 m 2 + 1 là tam thức bậc hai có ∆ = 13 m 2 - 4
Do đó hàm số có hai điểm cực trị khi và chỉ khi y ' có hai nghiệm phân biệt
⇔ g ( x ) có hai nghiệm phân biệt

x 1 ; x 2 là các nghiệm của g(x) nên theo định lý Vi-ét, ta có
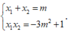

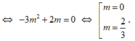
Đối chiếu với điều kiện (1), ta thấy chỉ m = 2 3 thỏa mãn yêu cầu bài toán
Đáp án C.
TXĐ: D = R.
Ta có y’ = 6x2 + 6x - 12, y’ = 0 ó 6x2 + 6x – 12 = 0 ó x = 1 hoặc x = -2.
y’’ = 12x + 12, y’’(1) = 24 > 0 => x2 = 1 là điểm cực tiểu, y’’(-2) = -12 < 0 => x1 - 2 là điểm cực đại.
Vậy ta có x2 – x1 = 3.