Q: Tìm giá trị của biểu thức:
(Lưu ý: Giải thích hộ mik vì mik ko hỉu rõ câu này lắm )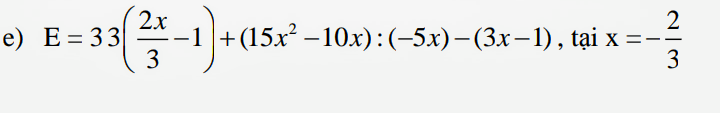
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
T
1
Những câu hỏi liên quan
dạng toán này mik kém lắm nên các bn đừng là tắt, mik ko hỉu đc:<
29 tháng 4 2021
Tham khảo link : https://hoc24.vn/cau-hoi/bai-6-tim-n-thuoc-z-de-phan-so-a-dfrac20n-134n-3a-a-co-gia-tri-nho-nhat-b-a-co-gia-tri-nguyen.160524630905
25 tháng 9 2016
|2x-1|> hoặc bằng 0
|2x-1-5> hoặc bằng -5
dấu bằng xảy ra khi x=3
Vậy Min B là -5 khi x=3
4 tháng 6 2016
a = 51 x 48 = 51 x ( 45 + 3 ) = 51 x 45 + 51 x 3
b = 54 x45 = (51 + 3 ) x 45 = 51 x45 + 3 x 45
ta thấy: 3 x 51 > 3 x 45 nên a > b
KK
4 tháng 6 2016
Ta có: A=51x48=51x(45+3) = 51x45+3x51
B= 54x45=(51+3)x45=51x45+3x45
Ta thấy 51x3>45x3 => 51x45+3x51>51x45+3x45 hay A>B
16 tháng 7 2018
Bài 2:
\(P=2010-\left(x+1\right)^{2008}\)
Ta có: \(\left(x+1\right)^{2008}\ge0\forall x\)
\(\Rightarrow2010-\left(x+1\right)^{2008}\le2010\forall x\)
\(P=2010\Leftrightarrow\left(x+1\right)^{2008}=0\Leftrightarrow x=-1\)
Vậy \(x=-1\)thì \(B_{max}=2010\)
16 tháng 7 2018
Bài 1:
\(D=\frac{x+5}{|x-4|}\)
Ta có: \(|x-4|\ge0\forall x\)
\(\Rightarrow D=\frac{x+5}{|x-4|}=\frac{x+5}{x-4}=\frac{x-4+9}{x-4}=1+\frac{9}{x-4}\)
Vì 1 không đổi
Nên để D đạt GTNN thì: \(\frac{9}{x-4}\)phải đạt GTLN
\(\Rightarrow x-4\)phải đạt GTLN
\(\Rightarrow x=13\)
GTNN của \(D=1+\frac{9}{x-4}=1+\frac{9}{13-4}=1+\frac{9}{9}=1+1=2\)
Vậy x=3 thì D đạt GTNN
Bài 2:
\(P=2010-\left(x+1\right)^{2008}\)
Ta có: \(\left(x+1\right)^{2008}\ge0\forall x\)
\(\Rightarrow2010-\left(x+1\right)^{2008}\le2010-0\)
\(\Rightarrow P\le2010\)
\(\Rightarrow\)GTLN của P=2010
\(\Leftrightarrow\left(x+1\right)^{2008}=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Vậy x=-1 thì P đạt GTLN
9 tháng 9 2021
\(a,-\left|2x-3\right|\le0,\forall x\Leftrightarrow-\left|2x-3\right|+3\le3\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(b,-\left|2-3x\right|\le0,\forall x\Leftrightarrow-\left|2-3x\right|-5\le-5\)
Dấu \("="\Leftrightarrow x=\dfrac{2}{3}\)
9 tháng 9 2021
a: \(A=-\left|2x-3\right|+3\le3\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
b: \(B=-\left|2-3x\right|-5\le-5\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{3}\)
15 tháng 1 2017
ta có 8*(x-2009)^2 >= 0 nên 25 - y^2 >=0 hay 5 >=y >=
+ y = 5 => x = 2009
+ y = 4 => ko thỏa mãn
+ y = 3...
+ y = 2..
+ y =1..
+ y = 0..
=> nghiệm duy nhất x = 2009 và y =5
\(E=22x-23-5x+2-3x+1\)
\(=14x-20\)
\(=14\cdot\dfrac{-2}{3}-20=\dfrac{-28}{3}-\dfrac{60}{3}=-\dfrac{88}{3}\)