Cho 2 số thực dương \(x;y\) và \(x>y\). Chứng minh rằng \(x+2y+\dfrac{216}{\left(x-y\right).\left(3y+2\right)}\ge16\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
21 tháng 12 2019
Đáp án C
Ta có
![]()

Khi đó

![]()
Vậy giá trị nhỏ nhất của biểu thức P là 3 + 2 2

CM
11 tháng 10 2017
Đáp án D
Các đáp án A, B, C đều đúng, chỉ có D là sai.
Chọn phương án D.
PN
0

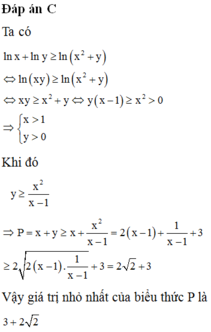



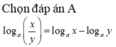
\(A=x+2y+\dfrac{216}{\left(x-y\right)\left(3y+2\right)}=x-y+3y+2+\dfrac{216}{\left(x-y\right)\left(3y+2\right)}-2\)\(\)
\(\Rightarrow x-y+3y+2+\dfrac{216}{\left(x-y\right)\left(3y+2\right)}\ge3\sqrt[3]{\left(x-y\right)\left(3y+2\right).\dfrac{216}{\left(x-y\right)\left(3y+2\right)}}\ge3\sqrt[3]{6^3}\ge18\)
\(\Rightarrow x-y+3y+2+\dfrac{216}{\left(x-y\right)\left(3y+2\right)}-2\ge18-2\ge16\)
\(\Rightarrow A\ge16\left(dpcm\right)\) \(dấu"="\) \(xảy\) \(ra\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{22}{3}\\y=\dfrac{4}{3}\end{matrix}\right.\)