Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi thời gian người 1 làm 1 mk xong cv là x ( h, x>6)
thời gian người 2 làm 1 mk xong cv là y (h, y>6)
Trong 1h, người 1 làm đc \(\frac{1}{x}\left(cv\right)\)
người 2 làm đc \(\frac{1}{y}\left(cv\right)\)
cả 2 người cùng làm đc \(\frac{1}{6}\left(cv\right)\)
Do đó ta có pt: \(\frac{1}{x}+\frac{1}{y}=\frac{1}{6}\left(1\right)\)
Nếu làm riêng rẽ, mỗi người nửa cv thì người 1 làm xong cv trong \(\frac{1}{2}:\frac{1}{x}=\frac{x}{2}\left(h\right)\), người 2 làm xong cv trong \(\frac{1}{2}:\frac{1}{y}=\frac{y}{2}\left(h\right)\)
Khi đó tổng số giờ làm việc là 12h30' \(\left(=\frac{25}{2}h\right)\)nên ta có pt \(\frac{x}{2}+\frac{y}{2}=\frac{25}{2}\Leftrightarrow x+y=25\left(2\right)\)
Từ (1)(2) ta có hpt \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{6}\\x+y=25\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=25-y\\\frac{1}{25-y}+\frac{1}{y}=\frac{1}{6}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=25-y\\6y-6y+150=25y-y^2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=25-y\\150-25y+y^2=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=25-y\\\left(10-y\right)\left(15-y\right)=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=10;x=15\\y=15;x=10\end{cases}}\left(TMĐK\right)\)
Vậy thời gian 2 người làm 1 mk xog cv lần lượt là 10h và 15h hoặc 15h và 10h
Gọi thời gian người 2 làm một mình là x
=>Thời gian người 1 làm một mình là x+5
Theo đề, ta có: \(\dfrac{1}{x}+\dfrac{1}{x+5}=\dfrac{1}{6}\)
=>\(\dfrac{x+5+x}{x\left(x+5\right)}=\dfrac{1}{6}\)
=>x^2+5x=6(2x+5)
=>x^2-7x-30=0
=>(x-10)(x+3)=0
=>x=10
=>Người 1 cần 15h
Gọi x(giờ) và y(giờ) lần lượt là thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình(Điều kiện: x>16; y>16)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người thợ làm được: \(\dfrac{1}{16}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\)(1)
Vì khi người thứ nhất làm trong 3 giờ, người thứ 2 làm trong 6 giờ thì hoàn thành được 25% công việc nên ta có phương trình:
\(\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{3}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-3}{y}=\dfrac{-1}{16}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=48\\\dfrac{1}{x}=\dfrac{1}{16}-\dfrac{1}{y}=\dfrac{1}{16}-\dfrac{1}{48}=\dfrac{1}{24}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=48\end{matrix}\right.\)(thỏa ĐK)
Vậy: Người thợ thứ nhất cần 24 giờ để hoàn thành công việc khi làm một mình
Người thợ thứ hai cần 48 giờ để hoàn thành công việc khi làm một mình
Gọi thời gian để người thứ nhất và người thứ hai một mình hoàn thành công việc lần lượt là x (giờ) và y (giờ). (Điều kiện x, y > 16).
⇒ Trong một giờ, người thứ nhất làm được 
(công việc); người thứ hai làm được 
(công việc).
+ Cả hai người cùng làm sẽ hoàn thành công việc trong 16 giờ nên ta có phương trình 
+ Người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì hoàn thành 
công việc nên ta có phương trình 
Vậy ta có hệ phương trình 
Đặt 
, hệ phương trình trở thành:
Gọi thời gian người thứ nhất, người thứ 2 làm công việc đó lần lượt là \(x;y>0\), giờ
Người thứ nhất làm xong ít hơn người thứ 2 là 6 giờ
\(y-x=6\Rightarrow y=x+6\)giờ
Trong 1 giờ đội thứ nhất làm được : \(\dfrac{1}{x}\)công việc
Trong 1 giờ đội thứ 2 làm được : \(\dfrac{1}{y}=\dfrac{1}{x+6}\)công việc
Do 2 người cùng làm 1 công việc thì 4 giờ xong
hay ta có phương trình \(\dfrac{1}{x}+\dfrac{1}{x+6}=\dfrac{1}{4}\Leftrightarrow\dfrac{x+6+x}{x\left(x+6\right)}=\dfrac{1}{4}\)( ĐK : \(x\ne-6;0\))
\(\Rightarrow8x+24=x\left(x+6\right)\Leftrightarrow\left(x-6\right)\left(x+4\right)=0\Leftrightarrow x=6\left(chon\right);x=-4\left(loai\right)\)
\(\Rightarrow y=6+6=12\)
Vậy người thứ nhất làm riêng công việc đó trong 6 giờ
người thứ 2 làm riêng công việc đó trong 12 giờ
Gọi thời gian người 1 làm riêng là x (giờ) (x>0, x thuộc N)
thời gian người 2 làm riêng là y (giờ) (y>0, y thuộc N)
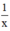Trong 1 giờ người 1 làm được \(\frac{1}{x}\)(công việc)
người 2 làm được \(\frac{1}{y}\)(công việc)
Trong 1 giờ cả 2 người làm được \(\frac{1}{x}+\frac{1}{y}=\frac{1}{16}\)(công việc) (1)
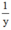Nếu người 1 làm 3h, người 2 là 6h thì hoàn thành 25% = \(\frac{1}{4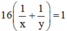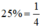}\)công việc nên ta có: \(\frac{3}{x}+\frac{6}{y}=\frac{1}{4}\)(2)
Từ (1) và (2) ta có hệ phương trình: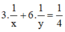
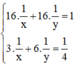
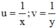\(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{16}\\\frac{3}{x}+\frac{6}{y}=\frac{1}{4}\end{cases}}\) Đặt \(\frac{1}{x}=a\)\(;\)\(\frac{1}{y}=b\)
\(\Rightarrow\hept{\begin{cases}a+b=\frac{1}{16}\\3a+6b=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}3a+3b=\frac{3}{16}\\3a+6b=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}3b=\frac{1}{16}\\a+b=\frac{1}{16}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=\frac{1}{48}\\a+\frac{1}{48}=\frac{1}{16}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=\frac{1}{48}\\a=\frac{1}{24}\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=24\\y=48\end{cases}}\)
Vậy......
Gọi thời gian để người thứ nhất và người thứ hai một mình hoàn thành công việc lần lượt là x (giờ) và y (giờ). (Điều kiện x, y > 16).
⇒ Trong một giờ, người thứ nhất làm được 1/x (công việc); người thứ hai làm được 1/y (công việc).
+ Cả hai người cùng làm sẽ hoàn thành công việc trong 16 giờ nên ta có phương trình 16 1 x + 1 y = 1
+ Người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì hoàn thành 25 % = 1 4 công việc nên ta có phương trình 3 ⋅ 1 x + 6 ⋅ 1 y = 1 4
Vậy ta có hệ phương trình 16 ⋅ 1 x + 16 ⋅ 1 y = 1 3 ⋅ 1 x + 6 ⋅ 1 y = 1 4
Đặt u = 1 x ; v = 1 y , hệ phương trình trở thành: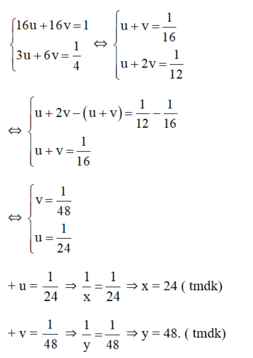
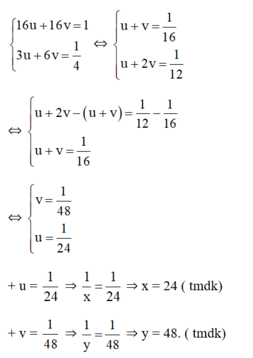
Vậy nếu làm riêng, người thứ nhất hoàn thành công việc sau 24 giờ và người thứ hai hoàn thành công việc trong 48 giờ.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
- Gọi x ( giờ ) là thời gian người thứ nhất hoàn thành xong công việc
- Gọi y ( giờ) là thời gian người thứ 2 hoàn thành xong công việc ( x,y > 0 )
- Trong 1h : người thứ nhất làm được \(\frac{1}{x}\)( công việc )
người thứ hai làm được \(\frac{1}{y}\)( công việc )
Ta có PT : \(\frac{1}{x}+\frac{1}{y}=\frac{1}{16}\left(1\right)\)
- Nếu người thứ nhất lúc đầu chỉ làm 3h và người thứ 2 làm trong 6h thì chỉ được 25% công việc
\(\frac{3}{x}+\frac{6}{x}=\frac{1}{4}\left(2\right)\)
- Từ (1) và (2) , ta có HPT : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{16}\\\frac{3}{x}+\frac{6}{y}=\frac{1}{4}\end{cases}}\)
Đặt \(\frac{1}{x}=u;\frac{1}{y}=v\), ta có :
\(\hept{\begin{cases}u+v=\frac{1}{16}\\3u+6v=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}6u+6v=\frac{3}{8}\\3u+6v=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}-3u=-\frac{1}{8}\\3u+6v=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}u=\frac{1}{24}\\\frac{1}{8}+6v=\frac{1}{4}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}u=\frac{1}{4}\\6v=\frac{1}{8}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{1}{24}\\\frac{1}{y}=\frac{1}{48}\end{cases}\Leftrightarrow\hept{\begin{cases}x=24\\y=48\end{cases}}}\)( TM )
Vậy : người thứ nhất làm xong trong 24h
người thứ 2 làm xong trong 48h
Gọi thời gian người thứ nhất làm riêng để xong nửa công việc là x; thời gian người thứ hai làm riêng để xong nửa công việc là y (giờ; x, y > 0)
Nếu làm riêng, mỗi người nửa việc thì tổng thời gian 2 người làm là 12,5 giờ nên ta có phương trình: x + y = 12,5 (1)
Thời gian người thứ nhất làm riêng để xong cả công việc là 2x, của người thứ 2 là 2y. Mà 2 người cùng làm thì trong 6 giờ xong việc nên ta có phương trình:
Vậy nếu làm riêng thì một người làm trong 2.7,5 = 15 giờ, còn người kia làm trong 2.5 = 10 giờ
Đáp án: D