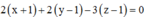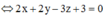Trong không gian Oxyz, cho tam giác ABC với A(
-
1;0;2), B(1;2;-1), C(3;1;2). Mặt phẳng (P) đi qua trọng tâm của tam giác ABC và vuông góc với đường thẳng AB là: A.
(
P
)
:
x
+
y
-
z
-
3
=
0
B.
(
P
)
:
2
x
+
2
y
-
3
z
+
3
=
0
C.
(
P
)
:
2
x
+
2
y
-
...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC với A( - 1;0;2), B(1;2;-1), C(3;1;2). Mặt phẳng (P) đi qua trọng tâm của tam giác ABC và vuông góc với đường thẳng AB là:
A. ( P ) : x + y - z - 3 = 0
B. ( P ) : 2 x + 2 y - 3 z + 3 = 0
C. ( P ) : 2 x + 2 y - 3 z + 1 = 0
D. ( P ) : 2 x + 2 y + 3 z - 3 = 0
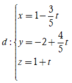
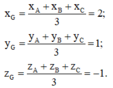
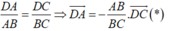
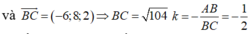
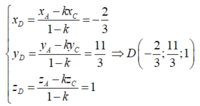
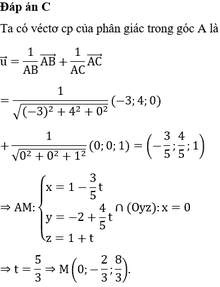
Đáp án B
Phương pháp: - Trọng tâm G của tam giác ABC có tọa độ được tính:
- Phương trình mặt phẳng đi qua M x 0 ; y 0 ; z 0 và có 1 VTPT n → ( a ; b ; c ) : a(x - x0)+b(y - y0)+c(z - z0) = 0
Cách giải: Trọng tâm G của tam giác ABC: G - 1 ; 1 ; 1
(P) vuông góc với AB => (P) nhận A B → 2 ; 2 ; - 3 là một VTPT
Phương trình mặt phẳng (P):
