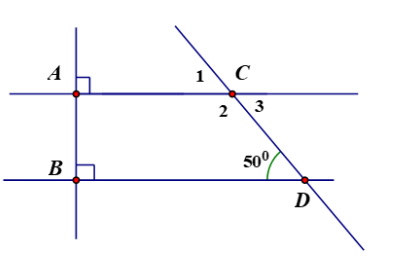
a) Chứng minh AC//BD
b) Tính C1;C2;C3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xet ΔBKD vuông tại K và ΔBHA vuông tại H có
góc B chung
=>ΔBKD đồng dạng với ΔBHA
=>BK/BH=BD/BA
=>BK*BA=BH*BD; BK/BD=BH/BA
b: Xét ΔBKH và ΔBDA có
BK/BD=BH/BA
góc B chung
=>ΔBKH đồng dạng với ΔBDA

đường thẳng m cắt AC và BD tại A và B
mà m đi qua 2 đường thẳng và tạo thành 2 cặp góc vuông
⇒AC//BD
-vì AC//BD và P cắt AC và BD tại C và D
-theo định luật 1 đường thẳng cắt hai đường thẳng thì sẽ có cặp góc đồng vị bằng nhau
⇒ C=D (=70o)

a: Xét ΔBKD vuông tại K và ΔBHA vuông tạiH có
góc KBD chung
=>ΔBKD đồng dạng với ΔBHA
=>BK/BH=BD/BA
=>BK*BA=BH*BD; BK/BD=BH/BA
b: Xét ΔBKH và ΔBDA có
BK/BD=BH/BA
góc KBH chung
=>ΔBKH đồng dạng với ΔBDA
c: ΔBKH đồng dạng với ΔBDA
=>\(\dfrac{S_{BKH}}{S_{BDA}}=\left(\dfrac{BH}{BA}\right)^2=\dfrac{4}{9}\)
=>\(S_{BDA}=64:\dfrac{4}{9}=144\left(cm^2\right)\)

a) Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔBAD=ΔBHD(cạnh huyền-góc nhọn)
Suy ra: BA=BH(hai cạnh tương ứng) và AD=HD(Hai cạnh tương ứng)
Ta có: BA=BH(cmt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AD=HD(cmt)
nên D nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BD là đường trung trực của AH
\(\Leftrightarrow AH\perp BD\)(đpcm)
b) Xét ΔDAH có DA=DH(cmt)
nên ΔDAH cân tại D(Định nghĩa tam giác cân)
\(\Leftrightarrow\widehat{DAH}=\dfrac{180^0-\widehat{ADH}}{2}\)(Số đo của một góc ở đáy trong ΔDAH cân tại D)
\(\Leftrightarrow\widehat{DAH}=\dfrac{180^0-110^0}{2}=35^0\)
Ta có: \(\widehat{BAH}+\widehat{DAH}=\widehat{BAD}\)(tia AH nằm giữa hai tia AD,AB)
\(\Leftrightarrow\widehat{BAH}+35^0=90^0\)
hay \(\widehat{BAH}=55^0\)
Vậy: \(\widehat{BAH}=55^0\)

a: Sửa đề: Tính BC
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=5^2+12^2=169\)
=>\(BC=\sqrt{169}=13\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔABD vuông tại A có
AB chung
AC=AD
Do đó: ΔABC=ΔABD
c: Ta có: ΔABC=ΔABD
=>\(\widehat{ABC}=\widehat{ABD}\)
Xét ΔBEA vuông tại E và ΔBFA vuông tại F có
BA chung
\(\widehat{EBA}=\widehat{FBA}\)
Do đó: ΔBEA=ΔBFA
=>AE=AF
=>ΔAEF cân tại A
a) Ta có: AC⊥AB,BD⊥AB
=> AC//BD
b) Ta có: AC//BD
\(\Rightarrow\widehat{C_1}=\widehat{D}=50^0\)(đồng vị)
Ta có: \(\widehat{C_2}=180^0-\widehat{C_1}=180^0-50^0=130^0\)(kề bù)
Ta có: \(\widehat{C_3}=\widehat{C_1}=50^0\)(đối đỉnh)