mn ơi giúp e câu này vs ạ e cảm ơn

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



câu a, \(\dfrac{x}{x+1}\); \(\dfrac{x^2}{1-x}\); \(\dfrac{1}{x^2-1}\) (đk \(x\)≠ -1; 1)
\(x^2\) - 1 = ( \(x\) - 1).(\(x\) + 1)
\(\dfrac{x}{x+1}\) = \(\dfrac{x.\left(x-1\right)}{\left(x+1\right).\left(x-1\right)}\);
\(\dfrac{x^2}{1-x}\) = \(\dfrac{-x^2}{x-1}\)= \(\dfrac{-x^2.\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{1}{x^2-1}\) = \(\dfrac{1}{\left(x-1\right)\left(x+1\right)}\)
b, \(\dfrac{10}{x+2}\); \(\dfrac{5}{2x-4}\); \(\dfrac{1}{6-3x}\) (đk \(x\) ≠ -2; 2)
2\(x-4\) = 2.(\(x\) - 2); 6 - 3\(x\) = - 3.(\(x\) - 2)
\(\dfrac{10}{x+2}\) = \(\dfrac{10.2.3\left(x-2\right)}{2.3\left(x+2\right)\left(x-2\right)}\) = \(\dfrac{60\left(x-2\right)}{6\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{5}{2x-4}\) = \(\dfrac{5.3\left(x+2\right)}{2.3\left(x-2\right).\left(x+2\right)}\) = \(\dfrac{15.\left(x+2\right)}{6.\left(x-2\right)\left(x+2\right)}\)
\(\dfrac{1}{6-3x}\) = \(\dfrac{-1}{3.\left(x-2\right)}\) = \(\dfrac{-1.\left(x+2\right)}{3.2.\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-2.\left(x+2\right)}{6.\left(x-2\right).\left(x+2\right)}\)
c, \(\dfrac{x}{2x-4}\); \(\dfrac{1}{2x+4}\) và \(\dfrac{3}{4-x^2}\) đk \(x\) ≠ 2; -2
\(\dfrac{x}{2x-4}\) = \(\dfrac{x}{2.\left(x-2\right)}\) = \(\dfrac{x.\left(x+2\right)}{2.\left(x-2\right).\left(x+2\right)}\)
\(\dfrac{1}{2x+4}\) = \(\dfrac{1}{2.\left(x+2\right)}\) = \(\dfrac{\left(x-2\right)}{2.\left(x+2\right).\left(x-2\right)}\)
\(\dfrac{3}{4-x^2}\) = \(\dfrac{-3}{\left(x-2\right)\left(x+2\right)}\) = \(\dfrac{-6}{2.\left(x-2\right)\left(x+2\right)}\)



a)\(2Ca+O_2\underrightarrow{t^o}2CaO\)
\(CaO+H_2O\rightarrow Ca\left(OH\right)_2\)
\(Ca\left(OH\right)_2+CO_2\rightarrow CaCO_3\downarrow+H_2O\)
\(CaCO_3\underrightarrow{t^o}CaO+CO_2\)
\(CaO+2HCl\rightarrow CaCl_2+H_2O\)

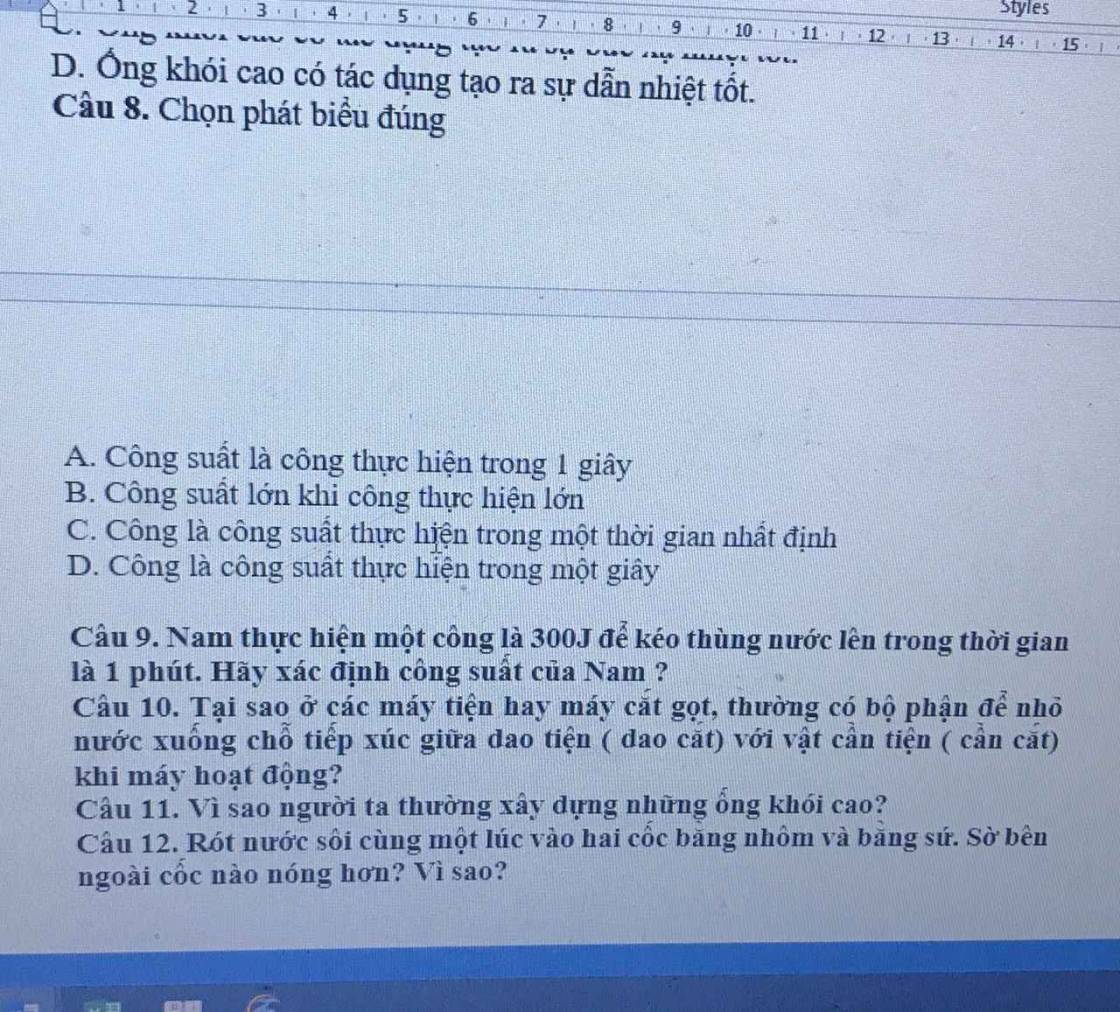
Câu 8: A
Câu 9: Tóm tắt:
\(A=300J\)
\(t=1p=60s\)
======
\(\text{℘ }=?W\)
Công suất của Nam:
\(\text{℘ }=\dfrac{A}{t}=\dfrac{300}{60}=5\left(W\right)\)
 gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ
gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ
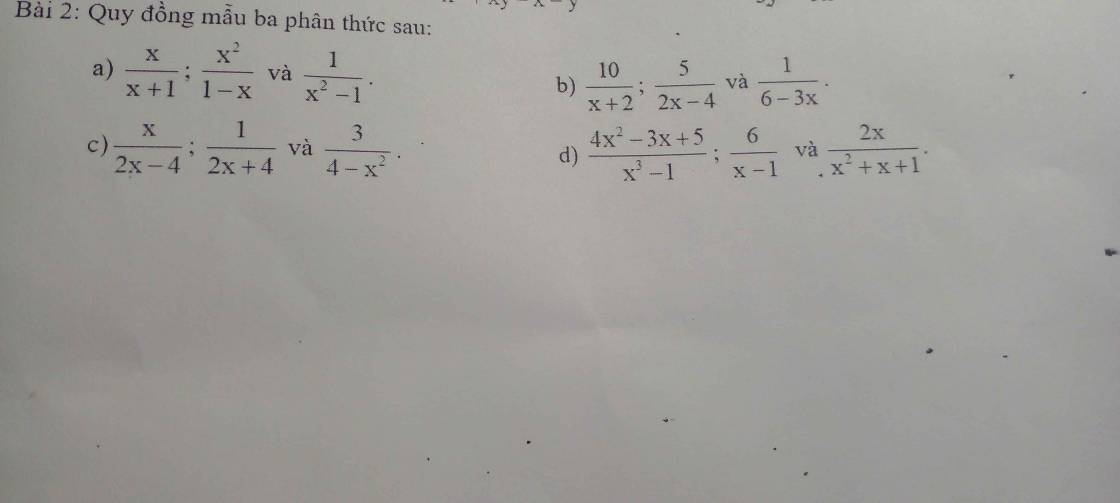

 Mn giúp e bài này vs ạ , e cảm ơn nhìu ạ!
Mn giúp e bài này vs ạ , e cảm ơn nhìu ạ! 

2: Để (d)//y=(m2+1)x-4 thì \(\left\{{}\begin{matrix}m^2=1\\m-5\ne-4\end{matrix}\right.\Leftrightarrow m=1\)