Cho hình chóp S.abc có tam giác ABC đều cạnh 2a ,SA vuông góc với đáy ,SA =a căn 3 .M và N lần lượt là trung điểm của SB, SC. Tính V. Samn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


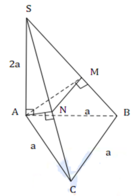
Đáp án A
Xét tam giác SAC vuông tại A có AP là đường cao, ta có:

Phương pháp:
Tính thể tích V S . A B C
Tính thể tích V S . A M N theo công thức tỉ lệ thể tích
Tính thể tích V A . B C M N và suy ra kết luận
Cách giải:
Xét tam giác SAB và SAC là các tam giác vuông tại A có hai cạnh góc vuông là a và 2a nên
![]()
Tam giác SAB vuông tại có đường cao AM
Khi đó ![]()
Tương tự ![]()
Lại có ![]()
Mặt khác 
![]()
Do đó ![]()
![]()
Chọn C.

Đáp án D
Gọi d là tiếp tuyến của (C) tại điểm A(1:0).
Ta có: y ' = 3 x 2 − 6 x ⇒ y ' 1 = 3.
Suy ra: d : − 3 x − 1 + 0 ⇔ y = − 3 x + 3.

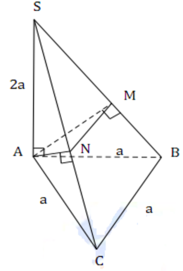
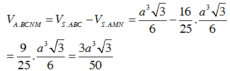

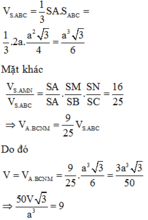
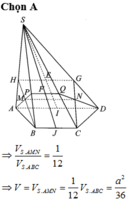
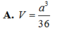
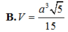

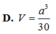
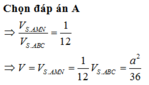
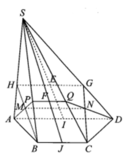
Gọi D là trung điểm BC. Nối SD cắt MN tại H
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AB;SA\perp AC;SA\perp AD\)
Xét tg vuông SAB và tg vuông SAC có
\(SB=\sqrt{SA^2+AB^2}=\sqrt{3a^2+4a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{3a^2+4a^2}=a\sqrt{7}\)
\(\Rightarrow SB=SC=a\sqrt{7};SA\) chung \(\Rightarrow\Delta SBC\) cân tại S
\(AM=\frac{SB}{2};AN=\frac{SC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)
Mà \(SB=SC\Rightarrow AM=AN\Rightarrow\Delta AMN\) cân tại A
Xét \(\Delta SBC\) có
MN là đường trung bình => MN//BC và \(MN=\frac{BC}{2}=a\)
SD là trung tuyến => SD cũng là đường cao của \(\Delta SBC\Rightarrow SD\perp BC\)
\(\Rightarrow SD\perp MN\) tại H (1)
Xét \(\Delta SMN\) có \(SM=\frac{SB}{2};SN=\frac{SC}{2}\) Mà \(SB=SC=a\sqrt{7}\Rightarrow SM=SN\Rightarrow\Delta SMN\) cân tại S
Mà \(SH\in SD\perp MN\Rightarrow HM=HN\) (trong tg cân đường cao đồng thời là đường trung tuyến)
Xét \(\Delta AMN\) có \(HM=HN\Rightarrow AH\perp MN\) (trong tg cân trung tuyến đồng thời là đường cao)
Nối AD có D là trung điểm BC => \(\Rightarrow AD\perp BC\) (trong tg cân trung tuyến đồng thời là đường cao)
Xét tg vuông ADB có
\(AD=\sqrt{AB^2-BD^2}=\sqrt{4a^2-a^2}=a\sqrt{3}=SA\Rightarrow\Delta SAD\) cân tại A
Áp dụng talet trong tg ta sẽ c/m được H là trung điểm của SD
Xét tg vuông cân SAD có
\(HS=HD\Rightarrow AH\perp SD\) (2)
Từ (1) và (2) \(\Rightarrow SD\perp\left(AMN\right);SH\in SD\Rightarrow SH\perp\left(AMN\right)\)
Xét tg vuông SBD có
\(SD=\sqrt{SB^2-BD^2}=\sqrt{7a^2-a^2}=a\sqrt{6}\)
\(SH=\frac{SD}{2}=\frac{a\sqrt{6}}{2}\)
Xét tg vuông SAD có
\(AH=\frac{SD}{2}=\frac{a\sqrt{6}}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nẳ cạnh huyền)
\(\Rightarrow S_{\Delta AMN}=\frac{MN.AH}{2}=\frac{a.a\sqrt{6}}{2.2}=\frac{a^2\sqrt{6}}{4}\)
\(\Rightarrow V_{SAMN}=\frac{1}{3}.S_{\Delta AMN}.SH=\frac{1}{3}.\frac{a^2\sqrt{6}}{4}.\frac{a\sqrt{6}}{2}=\frac{a^3}{4}\)
Cách khác:
Vì ABC đều => Diện tích ABC = \(\frac{\sqrt{3}}{4}AB^2=\sqrt{3}a^2\)
S. ABC có đường cao SA; đáy ABC
=> V (S.ABC) = \(\frac{1}{3}.SA.S_{ABC}=\frac{1}{3}.a\sqrt{3}.\sqrt{3}a^2=a^3\)
Vì M thuộc SB; N thuộc SC
=> \(\frac{V\left(S.AMN\right)}{V\left(S.ABC\right)}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=1.\frac{1}{2}.\frac{1}{2}=\frac{1}{4}\)
=> \(V\left(S.AMN\right)=\frac{a^3}{4}\)