[(8^2020)+(8^2019)]÷(8^2019)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BX
0
PK
2
24 tháng 3 2019
c) \(M=\frac{2019}{2020}+\frac{2020}{2021}\) và \(N=\frac{2019+2020}{2020+2021}\)
Ta có \(\frac{2019}{2020}>\frac{2019}{2020+2021}\)
\(\frac{2020}{2021}>\frac{2020}{2020+2021}\)
\(\Rightarrow\frac{2019}{2020}+\frac{2020}{2021}< \frac{2019+2020}{2020+2021}=N\)
\(\Rightarrow M>N\)
2 tháng 9 2021
\(\dfrac{8}{13}-\dfrac{7}{29}-\dfrac{8}{13}+\dfrac{7}{29}+\dfrac{2019}{2020}=\left(\dfrac{8}{13}-\dfrac{8}{13}\right)-\left(\dfrac{7}{29}+\dfrac{7}{29}\right)+\dfrac{2019}{2020}=0-0+\dfrac{2019}{2020}=\dfrac{2019}{2020}\)
PT
2
DC
9
NM
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 4 2023
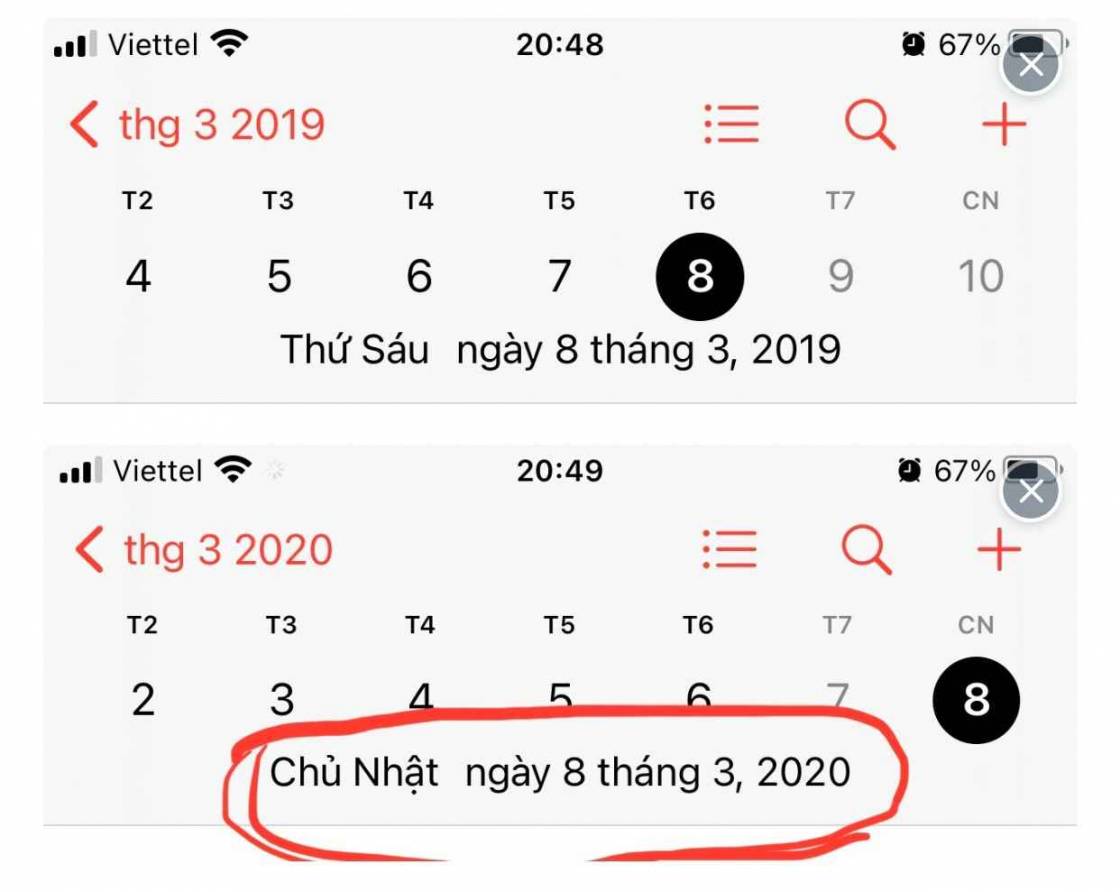
Vì năm 2020 là năm nhuận nên từ ngày 8/3/2019 đến ngày 8/3/2020 có 366 ngày
Vì 366 : 7 = 52 dư 2
mà 6 + 2 = 8
Vậy ngày 8/3 năm 2020 là ngày chủ nhật.
19 tháng 12 2019
Cho a,b,c khác 0 t/m:
1/a+1/b+1/c=1/2018 và a+b+c=2018
cmr" 1/a^2019+1/b^2019+1/c^2019=1/(a^2019+b^2019+c^2019)
Ta có :
gt⇒x2−xy−(5x−5y)−x+8=0⇒(x−y)(x−5)−(x−5)=−3⇒(5−x)(x−y−1)=3gt⇒x2−xy−(5x−5y)−x+8=0⇒(x−y)(x−5)−(x−5)=−3⇒(5−x)(x−y−1)=3
Đến đây là dạng của phương trình ước số bạn chỉ cần xét ước của 33 là sẽ tìm được nghiệm nguyên của PT
C
5
R
10 tháng 1 2022
S = 1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + ... + 2018 – 2019 - 2020 + 2021 + 2022
S = (1 + 2 - 3 - 4) + ... + (2017 + 2018 – 2019 - 2020) + 2021 + 2022
S = (-4) + ... + (-4) + 2021 + 2022
2020 : 4 = 505
S = (-4) . 505 + 2021 + 2022
S = (-2020) + 2021 + 2022
S = 2023
H9
HT.Phong (9A5)
CTVHS
13 tháng 8 2023
\(1-2+3-4+5-6+...+2019-2020+2021\)
\(=\left(1-2\right)+\left(3-4\right)+\left(5-6\right)+...+\left(2019-2020\right)+2021\)
\(=-1-1-1-..-1+2021\)
\(=-1\cdot1010+2021\)
\(=-1010+2021\)
\(=-1011\)
14 tháng 8 2023
1−2+3−4+5−6+...+2019−2020+2021
=(1−2)+(3−4)+(5−6)+...+(2019−2020)+2021=(1−2)+(3−4)+(5−6)+...+(2019−2020)+2021
=−1−1−1−..−1+2021=−1−1−1−..−1+2021
=−1⋅1010+2021=−1⋅1010+2021
=−1010+2021=−1010+2021
=−1011=−1011
\(\left(8^{2020}+8^{2019}\right):8^{2019}\)
\(=\frac{8^{2020}+8^{2019}}{8^{2019}}\)
\(=\frac{8^{2019}\cdot\left(8^1+1\right)}{8^{2019}}\)
\(=8^1+1\)
\(=8+1\)
\(=9\)