trong mp oxy cho ba đường thẳng d1: 2x-y+2=0, d2: 2x-y+1=0 và d3 :y-1=0 xác định tọa độ vecto v sao cho phép tịnh tiến T biến d1 thành d2 và biến d3 thành chính nó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
Vì d 1 không song song hoặc trùng với d 2 nên không tồn tại phép tịnh tiến nào biến d 1 thành d 2

Đáp án D
Vì d 1 không song song hoặc trùng với d 2 nên không tồn tại phép tịnh tiến nào biến d 1 thành d 2 .

a: 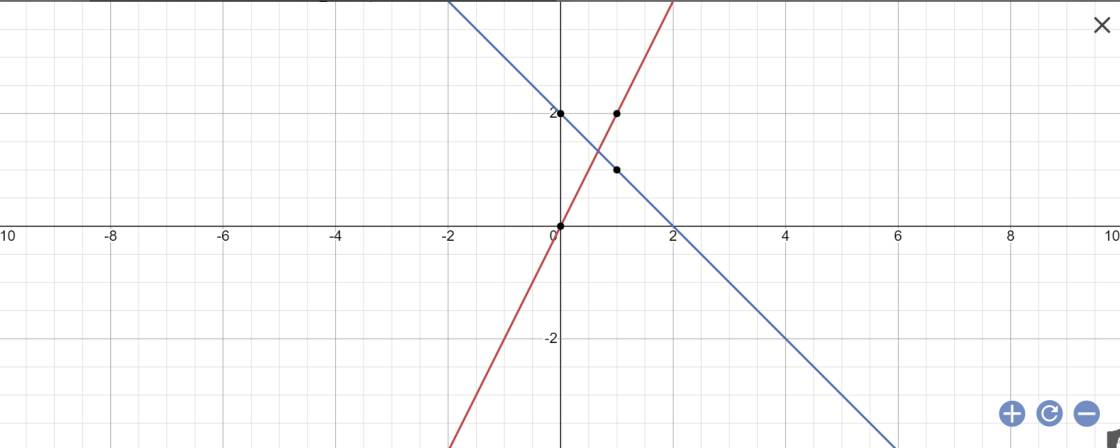
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=-x+b
Thay x=1 vào (d1), ta được:
\(y=2\cdot1=2\)
Thay x=1 và y=2 vào y=-x+b, ta được:
\(b-1=2\)
=>b=2+1=3

\(b,\text{PT hoành độ giao điểm: }-2x+5=x-1\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ \text{Vậy }A\left(2;1\right)\text{ là giao điểm }\left(d_1\right)\text{ và }\left(d_2\right)\\ c,\text{Gọi }\left(d_3\right):y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \left(d_3\right)\text{//}\left(d_1\right)\text{ và }M\left(-2;1\right)\in\left(d_3\right)\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne5\\-2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\\ \Leftrightarrow\left(d_3\right):y=-2x-1\)

d3//d2 \(\Rightarrow a=-1\)
d3 cắt d1 tại điểm có hoành độ bằng 1
\(\Rightarrow a+b=2\)
Ta có hệ
\(\left\{{}\begin{matrix}a=-1\\a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\)

Đáp án D
(d) biến thành chính nó khi vecto tịnh tiến cùng phương với (d). Mà (d) có một VTCP là 1 ; 2

Lời giải:
Phép tịnh tiến qua vecto $v$ biến $(d_3)$ thành chính nó thì $\overrightarrow{v}$ vecto chỉ phương của $(d_3)$
$\Rightarrow \overrightarrow{v}=(a,0)$
$T_{\overrightarrow{v}}(d_1)=d_2$
\(\Rightarrow \left\{\begin{matrix} 2x-y+2=0\\ 2(x+a)-y+1=0\end{matrix}\right.\Rightarrow a=\frac{1}{2}\)
Vậy $\overrightarrow{v}=(\frac{1}{2}, 0)$