Cho hình chữ nhật ABCD, M là một điểm bất kì nằm trong hình chữ nhật đó. Chứng minh MA + MC + MB + MD < AB+AD+AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Qua M kẻ NP vuông góc với AB ( N thuộc AB, P thuộc CD)
Ta có: MA+MB+MC+MD=(MA+MD)+(MB+MC) < AN+ND+NC+NB =AB+AC+AD (ĐPCM)

Lời giải:

Qua M kẻ \(FG\perp AB,CD\) như hình vẽ
Ta thấy $AFGD$ và $BFGC$ có các góc đều là góc vuông nên chúng là hình chữ nhật. Do đó \(AF=DG; BF=CG\)
Áp dụng định lý Pitago cho các tam giác vuông ta có:
\(\left\{\begin{matrix} MA^2=MF^2+FA^2\\ MB^2=MF^2+FB^2\\ MC^2=MG^2+GC^2\\ MD^2=MG^2+GD^2\end{matrix}\right.\)
\(\Rightarrow MA^2+MC^2-(MB^2+MD^2)=FA^2+GC^2-(FB^2+GD^2)\)
Do \(AF=DG; BF=CG\Rightarrow AF^2=DG^2; BF^2=GC^2\)
\(\Rightarrow FA^2+GC^2-(FB^2+GD^2)=0\)
\(\Leftrightarrow MA^2+MC^2-(MB^2+MD^2)=0\)
\(\Leftrightarrow MA^2+MC^2=MB^2+MD^2\)
Ta có đpcm

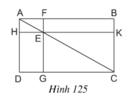
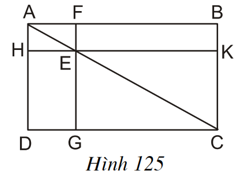
Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK,
ta đi chứng minh SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = AD.DC/2;
SABC = AB.BC/2.
ABCD là hình chữ nhật ⇒ AB = CD, AD = BC
⇒ SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH
⇒ AHEF là hình bình hành
Mà Â = 90º
⇒ AHEF là hình chữ nhật
⇒ SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
EK // GC, EG // KC
⇒ EGCK là hình bình hành
Mà D̂ = 90º
⇒ EGCK là hình chữ nhật
⇒ SEGC = SEKC (3).
Từ (1); (2); (3) suy ra đpcm.