Trong mặt phẳng Oxy, gọi a là đường phân giác góc phần tư thứ nhất, Cho (C): (x-2)2+(y+3)2=9, phép đối xứng trục a biến (C) thành (C') có PT là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phép đối xứng trục Oy biến tâm I(3;1) của (C) thành I’(-3;1); bán kính không thay đổi.
Chọn đáp án B.

a) a = c, b = - d
b) a = -c, b = d
c) a = d, b = c
d) a = -c, b = - d

Đường tròn (C) có tâm I(2; -4), bán kính R= 3
Đường tròn (C’) có tâm J( 3; -3) và bán kính R’ = 3
Vì R= R’ nên tồn tại phép đối xứng tâm: biến đường tròn (C) thành (C’).
Khi đó; tâm đối xứng K là trung điểm IJ.
x K = 2 + 3 2 = 5 2 y K = ( − 4 ) + ( − 3 ) 2 = − 7 2
⇒ K 5 2 ; - 7 2
Đáp án D

Đáp án C
(C) có tâm I(1;2) bán kính R = 3
Đ O : I → I’(–1;–2)
Phương trình đường tròn (C’): x + 1 2 + y + 2 2 = 3

Phép đối xứng qua trục Oy có :
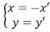
Thay vào phương trình (C) ta được x ' 2 + y ' 2 + 4 x ' + 5 y ' + 1 = 0 hay x 2 + y 2 + 4 x + 5 y + 1 = 0
Đáp án B
Gọi I là tâm (C) thì \(I\left(2;-3\right)\)
Phương trình a có dạng: \(x-y=0\)
Gọi d là đường thẳng qua I và vuông góc a
\(\Rightarrow\) phương trình d: \(1\left(x-2\right)+1\left(y+3\right)=0\Leftrightarrow x+y+1=0\)
Gọi M là giao điểm a và d \(\Rightarrow\left\{{}\begin{matrix}x-y=0\\x+y+1=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{1}{2};-\frac{1}{2}\right)\)
Gọi I' là ảnh của I qua phép đối xứng trục a thì I' là tâm (C')
M là trung điểm I'I \(\Rightarrow\left\{{}\begin{matrix}x_{I'}=2x_M-x_I=-3\\y_{I'}=2y_M-y_I=2\end{matrix}\right.\)
Phương trình (C'): \(\left(x+3\right)^2+\left(y-2\right)^2=9\)