Cho 2 điện trở R1 và R2.Biết rằng khi mắc nối tiếp thì điện trở tương đương của chúng là 100 ôm và khi mắc song song là 16 ôm tính R1 và R2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
29 tháng 9 2023
Khi mắc nối tiếp thì điện trở tương đương là 9Ω nên ta có:
\(R_{\text{tđ}}=R_1+R_2=9\Omega\) (1)
\(\Rightarrow R_2=9-R_1\left(2\right)\)
Khi mắt nối tiếp thì điện trở tương đương là 2Ω nên ta có:
\(R_{\text{tđ}}=\dfrac{R_1R_2}{R_1+R_2}=2\Omega\)
\(\Rightarrow R_1+R_2=\dfrac{R_1R_2}{2}\) (3)
Thay (3) vào (1) ta có:
\(\Rightarrow9=\dfrac{R_1R_2}{2}\Rightarrow R_1R_2=18\) (44)
Thay (3) vào (4) ta có:
\(R_1\cdot\left(9-R_1\right)=18\)
\(\Rightarrow9R_1-R^2_1=18\)
\(\Rightarrow R^2_1-9R_1+18=0\)
\(\Rightarrow\left[{}\begin{matrix}R_1=3\Omega\\R_1=6\Omega\end{matrix}\right.\)
TH1: \(R_1=3\Omega\)
\(\Rightarrow R_2=9-3=6\Omega\)
TH2: \(R_2=6\Omega\)
\(\Rightarrow R_2=9-6=3\Omega\)
VT
8 tháng 6 2018
– Công thức cần sử dụng:
Đối với đoạn mạch mắc nối tiếp: R t đ = R 1 + R 2
Đối với đoạn mạch mắc song song:
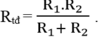
Khi R 1 nt R 2 ta có: R n t = R 1 + R 2 = 9 Ω ( 1 )
15 tháng 8 2021
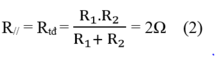
gọi R1,R2 lần lượt là x,y(ôm)
->hệ pt: \(\left\{{}\begin{matrix}x+y=100\\\dfrac{xy}{x+y}=16\end{matrix}\right.< =>\left\{{}\begin{matrix}y=100-x\left(1\right)\\\dfrac{x\left(100-x\right)}{x+100-x}=16\left(2\right)\end{matrix}\right.\)
giải pt(2)
\(=>\dfrac{100x-x^2}{100}=16< =>-x^2+100x-1600=0\)
\(\Delta=100^2-4\left(-1600\right)\left(-1\right)=3600>0\)
\(=>\left[{}\begin{matrix}x1=\dfrac{-100+60}{-2}=20\\x2=\dfrac{-100-60}{-2}=80\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}y1=80\\y2=20\end{matrix}\right.\)
vậy (R1;R2)={(20;80),(80;20)}
20 tháng 10 2021
1. a. Theo ht 4' trg đm //, ta có: Rtđ= (R1.R2)/(R1+R2)= (3.6)/(3+6)=2 ôm
b.Theo ĐL ôm, ta có: I= U/Rtđ=24/2=12 A
I1=U/R1=24/3=8 ôm
I2=U/R2=24/6=4 ôm
Khi mắc nối tiếp thì
\(R_{nt}=R_1+R_2=100\) Ω
Khi mắc song song thì
\(R_{ss}=\frac{R_1R_2}{R_1+R_2}=16\) Ω
\(\Rightarrow\left\{{}\begin{matrix}R_1+R_2=100\\R_1R_2=1600\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}R_1=20\Omega\\R_2=80\Omega\end{matrix}\right.\)
tại sao `R_{1}R_{2}=1600` vậy ạ