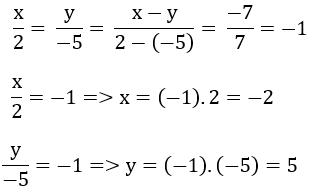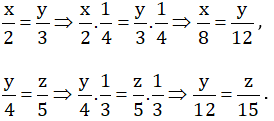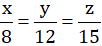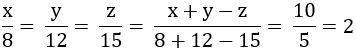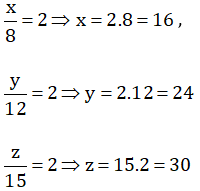ax(x−y)+y 3 (x+y) ( a a là số cho trước) tại x=4 x=4 và y=-2 y=−2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
2
19 tháng 9 2020
\(ax\left(x-y\right)+y^3\left(x+y\right)ax\left(x-y\right)+y3\left(x+y\right)\) tại x=2,y-3
\(ax\left(x-y\right)+y3\left(x+y\right)+axy^3\left(x^2-y^2\right)\)
Thay x=2,y=-3, có:
\(a2\left(2+3\right)-3.3\left(2-3\right)-a.2.3^3\left(2^2-3^3\right)\)
\(10a+9+270a\)
\(280a=-9\)
\(a=-\frac{9}{280}\)
19 tháng 9 2020
Mình lại ra là 15a+21 (sau khi rút gọn thành: \(ax^2-axy+xy^2+y^3\))
19 tháng 9 2020
ax( x - y ) + y2( x + y )
Thế x = 3 ; y = -2 ta được :
a.3.( 3 + 2 ) + (-2)2( 3 - 2 )
= a.3.5 + 4.1
= 15a + 4
25 tháng 7 2020
Thế x = 3 , y = -5 vào biểu thức ta được :
a.3[ 3 - ( -5 ) ] + ( -5 )4( 3 - 5 )
= a.3.8 + 625.( -2 )
= 24a - 1250
16 tháng 2 2021
a) Ta có: \(x:2=y:\left(-5\right)\)
nên \(\dfrac{x}{2}=\dfrac{y}{-5}\)
mà x-y=-7
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-1\\\dfrac{y}{-5}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)
Vậy: (x,y)=(-2;5)
b) Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}\)
nên \(\dfrac{x}{8}=\dfrac{y}{12}\)(1)
Ta có: \(\dfrac{y}{4}=\dfrac{z}{5}\)
nên \(\dfrac{y}{12}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
mà x+y-z=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{8}=2\\\dfrac{y}{12}=2\\\dfrac{z}{15}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)
Vậy: (x,y,z)=(16;24;30)
16 tháng 2 2021
b)
Do đó ta có 
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
