Cho tứ giác MNPQ biết \(\widehat{M}\)= x, \(\widehat{N}\)=2x, \(\widehat{P}\)=3x, \(\widehat{Q}\)=4x. Tính x ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
∠M + ∠N + ∠P + ∠Q = 360⁰ (tổng các góc trong tứ giác MNPQ)
⇒ ∠M + ∠N + ∠P + (∠P + 10⁰) = 360⁰
⇒ ∠M + ∠N + (∠N + 10⁰) + (∠N + 10⁰ + 10⁰) = 360⁰
⇒ ∠M + (∠M + 10⁰) + (∠M + 10⁰ + 10⁰) + (∠M + 10⁰ + 10⁰ + 10⁰)
⇒ ∠M + ∠M + 10⁰ + ∠M + 20⁰ + ∠M + 30⁰ = 360⁰
⇒ 4∠M + 60⁰ = 360⁰
⇒ 4∠M = 360⁰ - 60⁰
⇒ 4∠M = 300⁰
⇒ ∠M = 300⁰ : 4
⇒ ∠M = 75⁰
⇒ ∠N = 75⁰ + 10⁰ = 85⁰
⇒ ∠P = 85⁰ + 10⁰ = 95⁰
⇒ ∠Q = 95⁰ + 10⁰ = 105⁰
\(\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360^o\)
\(\widehat{M}+\widehat{M}+10+\widehat{M}+20+\widehat{M}+30=360\)
\(4\widehat{M}=360-60=300\Rightarrow M=75^o\)

Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên ta có:
\(\begin{array}{l}x + 2x + 3x + 4x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10\\x = 36^\circ \end{array}\)
Suy ra:
\(\widehat A = 36^\circ ;\;\widehat B = 72^\circ ;\;\widehat C = 108^\circ ;\;\widehat D = 144^\circ \)

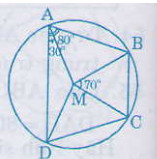
Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD

Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD

Theo bài ra ta có: \(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\widehat{\frac{D}{4}}\)
áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\frac{360^0}{10}=36\)
\(\Rightarrow\frac{\widehat{A}}{1}=36\Rightarrow\widehat{A}=36.1=36^0\)
\(\Rightarrow\frac{\widehat{B}}{2}=36\Rightarrow\widehat{B}=36.2=72^0\)
\(\Rightarrow\frac{\widehat{C}}{3}=36\Rightarrow\widehat{C}=36.3=108^0\)
\(\Rightarrow\frac{\widehat{D}}{4}=36\Rightarrow\widehat{D}=36.4=144^0\)

góc C-góc D=200-180=20 độ
góc C+góc D=120 độ
=>góc C=(20+120)/2=70 độ và góc D=120-70=50 độ
góc B=200-70=130 độ
góc A=180-70=110 độ
Xét tứ giác MNPQ ta có :
^M + ^N + ^P + ^Q = 3600 ( định lí )
<=> x + 2x + 3x + 4x = 3600
<=> 10x = 3600
<=> x = 360
=> ^M = 360
=> ^N = 360.2 = 720
=> ^P = 360.3 = 1080
=> ^Q = 360.4 = 1440
Vì tổng 4 góc trong 1 tứ giác là \(360^0\)
\(\Rightarrow\)\(\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360^0\)
\(\Leftrightarrow\)\(x+2x+3x+4x=360\)
\(\Leftrightarrow\)\(10x=360\)
\(\Leftrightarrow\)\(x=36\)
Vậy \(x=36^0\)