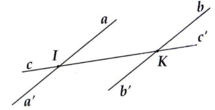
Cho hình vẽ trên. Tính các góc còn lại, biết góc aIK= IKb'= 28 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính được a I K ^ = a ' I c ^ = I K b ' ^ = b K c ' ^ = 28 ° a I c ^ = a ' I K ^ = b I K ^ = b ' K c ' ^ = 180 ° − 28 ° = 152 °

Ta có \(\widehat{aIK}=\widehat{IKb'}\Rightarrow aa'//bb'\)
=> \(\widehat{a'Ic}=\widehat{bKc'}=\widehat{aIK}=28^{\text{o}}\)
Lại có \(\widehat{a'IK}=180^{\text{o}}-\widehat{aIK}=180^{\text{o}}-28^{\text{o}}=152^{\text{o}}=\widehat{aIC}=\widehat{c'Kb'}\)
Vì IKb và IKb' là 2 góc kề bù \(\Rightarrow\)IKb = 180o - 28o = 152o
Vì aa' // bb' , IKb và KIa' là 2 góc so le trong bằng nhau \(\Rightarrow\)KIa' = 152o
Vì cIa và KIa' là 2 góc đối đỉnh \(\Rightarrow\)cIa = 152o
Vì cIa' và KIa là 2 góc đối đỉnh \(\Rightarrow\)cIa' = 28o
Vì IKb và b'Kc' là 2 góc đối đỉnh \(\Rightarrow\)b'Kc' = 152o
Vì IKb' và bKc' là 2 góc đối đỉnh \(\Rightarrow\)bKc' = 28o

a: Xét tứ giác AIHK có
\(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)
Do đó: AIHK là hình chữ nhật
b: \(\widehat{AIK}=\widehat{AHK}\)
mà \(\widehat{AHK}=\widehat{C}\)
nên \(\widehat{AIK}=\widehat{C}\)
c: Xét ΔAIK vuông tại A và ΔACB vuông tại A có
\(\widehat{AIK}=\widehat{C}\)
Do đó: ΔAIK∼ΔACB

a) Ta thấy : BAD = BCD = 120°( tính chất)
Mà AB//CD ( ABCD là hình bình hành)
=> ABC + BCD = 180°
=> ABC = ADC = 60°

a) Tứ giác AIHK có góc H=K=I=A=90độ
=> AIHK LÀ HÌNH CHỮ NHẬT ( tỨ GIÁC CÓ 3 GÓC VUÔNG)

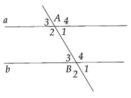
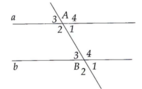
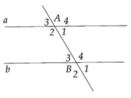
Tương tự 5. Tính được A 3 ^ = A 1 ^ = B 3 ^ = B 1 ^ = 60 ° A 2 ^ = A 4 ^ = B 2 ^ = B 4 ^ = 120 °

Tính được A 3 ^ = A 1 ^ = B 3 ^ = B 1 ^ = 60 ° A 2 ^ = A 4 ^ = B 2 ^ = B 4 ^ = 120 °

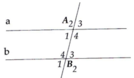
Ta có a //b nên B 1 ^ = A 1 ^ = 75° (hai góc đồng vị).
A 3 ^ = A 1 ^ = 75 ° ; B 3 ^ = B 1 ^ =75° (cặp góc đối đỉnh).
Lại có A 1 ^ + A 2 ^ = 180 ° (hai góc kề bù)
=> A 2 ^ = 180°- 75° = 105°.
B 4 ^ = A 2 ^ = 105° (hai góc đồng vị)
B 4 ^ = B 2 ^ = 105°; A 4 ^ = A 2 ^ = 105° (cặp góc đối đỉnh)