Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xuat phat la diem : A
chuyen huong: B
diem dung :C
∆ABC vuong tai B
van toc ca no la v (km/s)
AB=8/3.v
BC=10/3.v
AC=1
∆ABC vuong =>AC^2=AB^2+BC^2
<=>1=v^2 (8^2+10^2)/9=10^2.4^2.v^2=9/ (8^2+10^2)
v=3/√(164) (km/p)

Tóm tắt
Vnước= 5 km/h, Vngược_dòng= 20 km/h
a) tính Vthực
b) Cano gặp khúc gỗ đi ngược chiều tại A, cano đi ngược dòng đc 15 phút thì quay lại về phía A, biết V thực 2 lần như nhau, hỏi cano gặp lại khúc gỗ cách A bao nhiêu km
a) Vthực= Vngược + Vnước = 20 + 5 = 25 (km/h)
b)+) Khúc gỗ trôi là do nước chảy ===> V khúc gỗ chính là V nước
<=> Vgỗ = 5 km/h
+)Quãng đường cano đi đc 15 phút ngược dòng : S= 20 . 15/60 =5 (km)
Quãng đường gỗ đi đc 15 phút: 5. 15/60 =1,25 (km)
=> Khoảng cách Cano và gỗ sau 15 phút là: 5 + 1,25 = 6,25 (km)
+) Thời gian cano đổi kịp gỗ là \(\dfrac{Khoảng-cách}{Vxuôi.dòng-Vgỗ}\) = \(\dfrac{6,25}{\left(25+5\right)-5}\)= \(\dfrac{1}{4}\) (giờ)
+) Cano gặp lại gỗ tại điểm cách A
S= Tđi_đc . Vnước = \(\left(\dfrac{1}{4}+\dfrac{15}{60}\right).5=2,5\) (km)

Tham khảo:
Lấy các điểm: A, C sao cho:
Vectơ vận tốc dòng nước\(\overrightarrow {{v_n}} = \overrightarrow {OA} \)
Vectơ vận tốc chuyển động \(\overrightarrow {{v_{cano}}} = \overrightarrow {OC} \)
Ta có: \(\overrightarrow {{v_{cano}}} = \overrightarrow {{v_n}} + \overrightarrow v \), với \(\overrightarrow v \) là vectơ vận tốc riêng của cano.
Gọi B là điểm sao cho \(\overrightarrow v = \overrightarrow {OB} \) thì OACB là hình bình hành.

Vì tàu chuyển động theo hướng \(S{15^o}E\) nên vectơ \(\overrightarrow {OC} \) tạo với hướng Nam (tia OS) góc \({15^o}\) và tạo với hướng Đông (tia OE) góc \({90^o} - {15^o} = {75^o}\).
Mà nước trên sông chảy về hướng đông nên vectơ \(\overrightarrow {OA} \) cùng hướng với vectơ \(\overrightarrow {OE} \)
Do đó góc tạo bởi vectơ \(\overrightarrow {OC} \) và vectơ \(\overrightarrow {OA} \) là \({75^o}\)
Xét tam giác OAC ta có:
\(OA = \;|\overrightarrow {{v_n}} |\; = 3\); \(OC = \;|\overrightarrow {{v_{cano}}} |\; = 20\) và \(\widehat {AOC} = {75^o}\)
Áp dụng định lí cosin tại đỉnh O ta được:
\(\begin{array}{l}A{C^2} = O{A^2} + O{C^2} - 2.OA.OC.\cos \widehat {AOC}\\ \Leftrightarrow A{C^2} = {3^2} + {20^2} - 2.3.20.\cos {75^o} \approx 378\\ \Leftrightarrow OB = AC \approx 19,44\end{array}\)
Vậy vận tốc riêng của cano là 19,44 km/h

dòng sông chảy theo hướng A->B với \(v=2,5km/h\)
=> đây là vận tốc dòng nước
đổi \(1h30'=\dfrac{3}{2}h\)
\(=>v1=\dfrac{S}{t}=\dfrac{42}{\dfrac{3}{2}}=28km/h\)
mà ca nô đi từ A->B với vận tốc \(v1=28=vc+v=vc+2,5=>vc=v1-v=28-2,5\)\(=25,5km/h\)
đây là vận tốc thực ca nô
đi từ B->A \(=>v2=vc-2,5=25,5-2,5=23km/h\)
\(=>t1=\dfrac{S}{v2}=\dfrac{42}{23}\approx1,8h\)

Ta có : 2h5p=\(\frac{25}{12}h\)
Gọi vận tốc cano khi nước ko chảy là v (km/h)
Thời gian cano đi xuôi dòng từ A đến B là :
t1=\(\frac{AB}{v+v_0}=\frac{25}{v+5}\left(h\right)\)
Thời gian cano đi ngược dòng từ B về A là :
t2=\(\frac{AB}{v-v_0}=\frac{25}{v-5}\left(h\right)\)
Ta có : \(t_1+t_2=\frac{25}{12}\)(h)
\(\Rightarrow\frac{25}{v+5}+\frac{25}{v-5}=\frac{25}{12}\)
\(\Rightarrow25\left(\frac{1}{v+5}+\frac{1}{v-5}\right)=\frac{25}{12}\)
\(\Rightarrow\frac{v-5+v+5}{\left(v+5\right)\left(v-5\right)}=\frac{1}{12}\)
\(\Rightarrow\frac{2v}{v^2-5v+5v-25}=\frac{1}{12}\)
\(\Rightarrow24v=v^2-25\)
\(\Rightarrow v^2-24v-25=0\)
\(\Rightarrow v^2-25v+v-25=0\)
\(\Rightarrow v\left(v-25\right)+\left(v-25\right)=0\)
\(\Rightarrow\left(v-25\right)\left(v+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}v-25=0\\v+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}v=25\\v=-1\left(loại\right)\end{matrix}\right.\)
Vậy vận tốc cano khi nước lặng là 25km/h
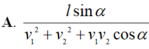
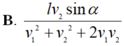
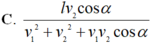
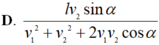

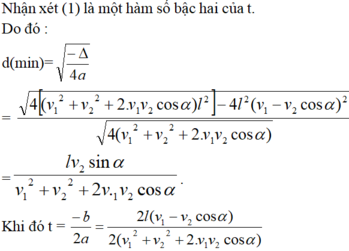
bạn ơi chiều bắc nam nhé mk đang bị mắc chỗ này á
thì ngược lại thui :v