Cho tam giác DEF vuông tại D. Gọi A,B lần lượt là hình chiếu của H trên DE, DF.
a) chứng minh tam giác DAB đồng dạng với tam giác DEF
b) kẻ trung tuyến DM. Chứng minh EDH=MDF
c) DM cắt AB tại O. Chứng minh DM vuông góc AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 8 2021
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔDHE vuông tại H có HA là đường cao ứng với cạnh huyền DE, ta được:
\(DA\cdot DE=DH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDFH vuông tại H có HB là đường cao ứng với cạnh huyền DF, ta được:
\(DB\cdot DF=DH^2\)(2)
Từ (1) và (2) suy ra \(DA\cdot DE=DB\cdot DF\)
hay \(\dfrac{DE}{DB}=\dfrac{DF}{DA}\)
Xét ΔDEF vuông tại D và ΔDBA vuông tại D có
\(\dfrac{DE}{DB}=\dfrac{DF}{DA}\)(cmt)
Do đó: ΔDEF\(\sim\)ΔDBA(c-g-c)
TT
15 tháng 5 2021
a) xét ΔHED và ΔDEF có
\(\widehat{EHD}=\widehat{EDF}=\)90o
\(\widehat{E} chung\)
=> ΔHED ∼ ΔDEF (gg)
b) Xét ΔDEF có \(\widehat{D}=\)90o
=> DE2+DF2=EF2
=>62+82=EF2
=> EF=10 cm
SΔDEF=\(\dfrac{ED.DF}{2}=\dfrac{DH.EF}{2}\)=> ED.DF=DH.EF => 6.8=DH.10
=> DH =4,8 cm
c) Xét ΔDEH có \(\widehat{EHD}=90\)o
=> HD2.HE2=ED2
=>4.82+HE2=62
=> HE=3.6
ta lại có DI là phân giác
=> \(\dfrac{EI}{IH}=\dfrac{ED}{HD}\)
=>\(\dfrac{EI}{EH-EI}=\dfrac{6}{4.8} \)=>\(\dfrac{EI}{3.6-EI}=\dfrac{6}{4.8}\)=>EI=2
=> IH=EH-EI=3.6-2=1.6
15 tháng 5 2021
a) Xét ΔHED vuông tại H và ΔDEF vuông tại D có
\(\widehat{HED}\) chung
Do đó: ΔHED\(\sim\)ΔDEF(g-g)
DN
23 tháng 5 2023
Xét `\Delta MHF` và `\Delta MKE`:
`\text {MH = MK (gt)}`
$\widehat {KME} = \widehat {HMF} (\text {đối đỉnh})$
`\text {ME = MF (trung tuyến DM)}`
`=> \Delta MHF = \Delta MKE (c-g-c).`
23 tháng 5 2023
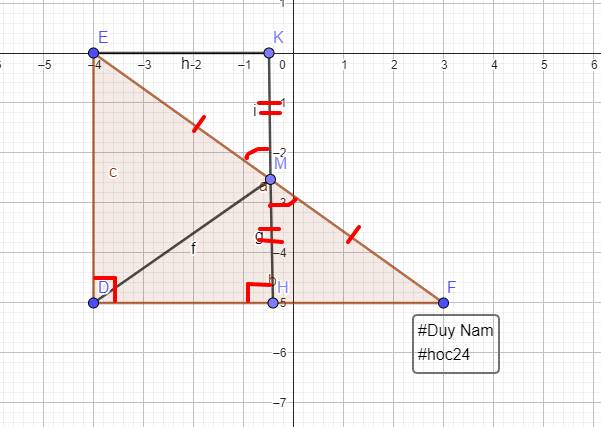
Xét ΔMHF và ΔMKE có
MH=MK
góc HMF=góc KME
MF=ME
=>ΔMHF=ΔMKE
