Question

[Nguyễn Châu Mỹ Linh]

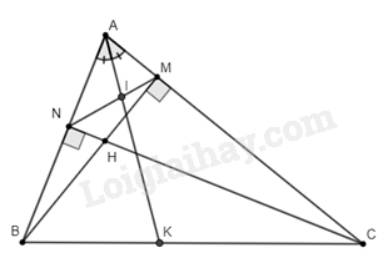
Cho \(\Delta\)ABC có góc A bằng \(60^o\), đường cao BN và CN cắt nhau tại H. NỐi AH cắt BC tại K. Biết AC = 8cm

a) Tính AN, NC và số đo của\(\widehat{ABM}\) và \(\widehat{BHC}\)

b) Chứng minh rằng AK\(\perp\)BC, \(\widehat{MBC}\) = \(\widehat{CAK}\)

c) Goi I là trung điểm của BC. Chứng minh rằng tam giác MIN đều

Answer 1

[Nguyễn Lê Phước Thịnh]

a) Xét ΔANC vuông tại N có

\(\widehat{NAC}+\widehat{ACN}=90^0\)(hai góc nhọn phụ nhau)

hay \(\widehat{ACN}=90^0-\widehat{NAC}=90^0-60^0=30^0\)

Xét ΔANC vuông tại N có \(\widehat{ACN}=30^0\)(cmt)

nên \(AN=\frac{AC}{2}\)(Trong một tam giác vuông, cạnh đối với góc 30⁰ thì bằng nửa cạnh huyền)

hay \(AN=\frac{8}{2}=4cm\)

Áp dụng định lí Pytago vào ΔANC vuông tại N, ta được:

\(AC^2=AN^2+NC^2\)

\(\Leftrightarrow NC^2=AC^2-AN^2=8^2-4^2=64-16=48\)

hay \(NC=4\sqrt{3}cm\)

Vậy: AN=4cm; \(NC=4\sqrt{3}cm\)

Xét ΔABM vuông tại M và ΔACN vuông tại N có

\(\widehat{BAM}\) chung

Do đó: ΔABM∼ΔACN(g-g)

\(\Rightarrow\widehat{ABM}=\widehat{ACN}\)(hai góc tương ứng bằng nhau)

mà \(\widehat{ACN}=30^0\)(cmt)

nên \(\widehat{ABM}=30^0\)

Vậy: \(\widehat{ABM}=30^0\)

b) Xét ΔABC có:

BM là đường cao ứng với cạnh AC(gt)

CN là đường cao ứng với cạnh AB(gt)

BM\(\cap\)CN={H}

Do đó: H là trực tâm của ΔABC(Tính chất ba đường cao của tam giác)

⇔AH⊥BC

hay AK⊥BC

Xét ΔCBM vuông tại M và ΔCAK vuông tại K có

\(\widehat{BCM}\) chung

Do đó: ΔCBM∼ΔCAK(g-g)

\(\Rightarrow\widehat{CBM}=\widehat{CAK}\)(hai góc tương ứng)(ddpcm)

c) Ta có: \(AN=\frac{AC}{2}\)(cmt)

nên \(\frac{AN}{AC}=\frac{1}{2}\)

hay \(\frac{AC}{AN}=2\)

Ta có: ΔABM∼ΔACN(cmt)

⇔\(\frac{AB}{AC}=\frac{AM}{AN}\)

hay \(\frac{AB}{AM}=\frac{AC}{AN}\)

Xét ΔABC và ΔAMN có

\(\frac{AB}{AM}=\frac{AC}{AN}\)(cmt)

\(\widehat{BAC}\) chung

Do đó: ΔABC∼ΔAMN(c-g-c)

⇒\(\frac{BC}{MN}=\frac{AC}{AN}\)(hai cặp cạnh tương ứng tỉ lệ)

mà \(\frac{AC}{AN}=2\)(cmt)

nên \(\frac{BC}{MN}=2\)

hay \(MN=\frac{BC}{2}\)(1)

Xét ΔNBC vuông tại N có NI là đường trung tuyến ứng với cạnh huyền BC(I là trung điểm của BC)

nên \(NI=\frac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(2)

Xét ΔMBC vuông tại M có MI là đường trung tuyến ứng với cạnh huyền BC(I là trung điểm của BC)

nên \(MI=\frac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(3)

Từ (1), (2) và (3) suy ra IN=IM=NM

Xét ΔINM có IN=IM=NM(cmt)

nên ΔINM đều(định nghĩa tam giác đều)(đpcm)