X/6 - 1/y =1/2
Tìm số nguyên x,y :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2:
a: 5/x-y/3=1/6
=>\(\dfrac{15-xy}{3x}=\dfrac{1}{6}\)
=>\(\dfrac{30-2xy}{6x}=\dfrac{x}{6x}\)
=>30-2xy=x
=>x(2y+1)=30
=>(x;2y+1) thuộc {(30;1); (-30;-1); (10;3); (-10;-3); (6;5); (-6;-5)}
=>(x,y) thuộc {(30;0); (-30;-1); (10;1); (-10;-2); (6;2); (-6;-3)}
b: x/6-2/y=1/30
=>\(\dfrac{xy-12}{6y}=\dfrac{1}{30}\)
=>\(\dfrac{5xy-60}{30y}=\dfrac{y}{30y}\)
=>5xy-60=y
=>y(5x-1)=60
=>(5x-1;y) thuộc {(-1;-60); (4;15); (-6;-10)}(Vì x,y là số nguyên)
=>(x,y) thuộc {(0;-60); (1;15); (-1;-10)}

Lời giải:
$117=(2y+1)^2-x^2=(2y+1-x)(2y+1+x)$
Vì $x,y$ nguyên nên $2y+1-x, 2y+1+x$ nguyên. Do đó ta có bảng sau:


\(\)áp dụng BĐT AM-GM(BÀi này ko có Max chỉ có Min)
\(=>\dfrac{1}{x}+\dfrac{1}{y}\ge2\sqrt{\dfrac{1}{xy}}=\dfrac{2}{\sqrt{xy}}\)
\(=>\dfrac{1}{2}\ge\dfrac{2}{\sqrt{xy}}=>\sqrt{xy}\ge4\)
\(=>S=\sqrt{x}+\sqrt{y}\ge2\sqrt{4}=4\)
dấu"=" xảy ra<=>x=y=4


Bài 2:
a: Thay x=1 và y=1 vào y=ax+5, ta được:
\(a\cdot1+5=1\)
=>a+5=1
=>a=-4
b: a=-4 nên y=-4x+5
| x | -2 | -1 | 0 | 1/2 | -3 |
| y=-4x+5 | 13 | 9 | 5 | 3 | -7 |
Bài 1:
a: \(y=-2\left(x+5\right)-4\)
\(=-2x-10-4\)
=-2x-14
a=-2; b=-14
b: \(y=\dfrac{1+x}{2}\)
=>\(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2};b=\dfrac{1}{2}\)
cho hệ pt 3x-y=2m-1 và x+2y=3m+2
tìm m để hpt có nghiệm ( x;y) thỏa mãn \(^{x^2}\)+\(^{y^2}\)đạt GTNN

Ta có: \(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m-2\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x=7m\\y=3x-2m+1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=m+1\end{matrix}\right.\)
Mặt khác: \(x^2+y^2=2m^2+2m+1=2\left(m^2+m+\dfrac{1}{2}\right)\)
\(=2\left(m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{4}\right)=2\left(m+\dfrac{1}{2}\right)^2+\dfrac{1}{2}\ge\dfrac{1}{2}\)
Dấu bằng xảy ra \(\Leftrightarrow m+\dfrac{1}{2}=0\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy ...

Chọn A
ĐKXĐ:
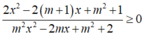
và m2x2 – 2mx+ m2+2≠ 0
+Xét tam thức bậc hai :
f(x) = 2x2 -2( m+1) x+ m2+1
Ta có hệ số a= 2> 0;
∆ = (m+1) 2- 2( m2+1) = -(m-1) 2 ≤ 0
Suy ra với mọi m ta có f(X) ≥ 0 vớ i mọi m(1)
+ Xét tam thức bậc hai:
g(x) = và m2x2 – 2mx+ m2+2
Với m= 0 ta có g(x) = 2> 0
xét với m≠ 0 ta có:
hệ số a= m2> 0
và ∆’ = m2- m2(m2+2) = -m2(m2+1) < 0
Suy ra với mọi m ta có g(x) > 0 với mọi x(2)
Từ (1) và (2) suy ra với mọi m thì
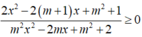
và m2x2 – 2mx+ m2+2≠ 0 đúng với mọi giá trị của x
Vậy tập xác định của hàm số là D = R
\(\frac{x}{6}-\frac{1}{y}=\frac{1}{2}\)
\(\Leftrightarrow\frac{x}{6y}-\frac{6}{6y}=\frac{3y}{6y}\)
\(\Leftrightarrow x-6=3y\)
\(\Leftrightarrow x=3\cdot\left(y+2\right)\)
\(\frac{x}{6}-\frac{1}{y}=\frac{1}{2}\Leftrightarrow\frac{1}{y}=\frac{x}{6}-\frac{1}{2}\Leftrightarrow\frac{1}{y}=\frac{x-3}{6}\)
\(\Leftrightarrow\left(x-3\right)y=6\Leftrightarrow x-3;y\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)