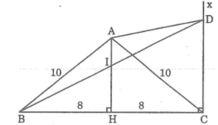
Cho tam giac ABC vuông tại A , BC=5, AB=2AC
. Từ A hạ đường cao AH lấy một điểm I sao cho AI =1/3 AH. Từ C kẻ đừờng thẳng Cx song song voi AH . Goi giao diem cua BI voi Cx là D. Tính dien tich của tứ giác AHCD
. Vẽ hai đường tròn (B, AB)và (C, AC). Goi giao diem khác A của 2 đường tròn này là E. CM : CE là tiếp tuyến của duong tròn (O)