Tìm tất cả các cặp số nguyên (x,y) thỏa mãn
a) x2+y2 = (xy-3)2 b) x2(y+1)+y2(x+1)=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
3
XO
25 tháng 7 2023
\(x^2+y^2+2\left(x+y\right)-xy=0\)
\(\Leftrightarrow4x^2-4xy+4y^2+8\left(x+y\right)=0\)
\(\Leftrightarrow\left(2x-y\right)^2+4\left(2x-y\right)+4+3y^2+12y+12=-16\)
\(\Leftrightarrow\left(2x-y+2\right)^2+3\left(y+2\right)^2=-16\)
Dễ thấy VT \(\ge0\) ; VP < 0 nên phương trình vô nghiệm
24 tháng 7 2023
\(x^2+y^2-2\left(x+y\right)=xy\)
\(\Rightarrow x^2-2x+1+y^2-2y+1=2+xy\)
\(\Rightarrow\left(x-1\right)^2+\left(y-1\right)^2=2+xy\)
Ta lại có : \(\left(x-1\right)^2+\left(y-1\right)^2\ge2\left(x-1\right)\left(y-1\right)\) (Bất đẳng thức Cauchy)
CM
1 tháng 5 2019
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
CM
2 tháng 6 2017
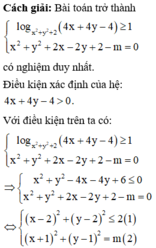
log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B
CM
6 tháng 10 2017
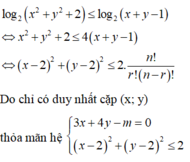
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
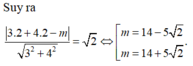
Chọn C.
a) Đặt x +y = S; xy = P => S; P nguyên
Ta có: \(x^2+y^2=\left(xy-3\right)^2\Leftrightarrow\left(x+y\right)^2-2xy=\left(xy\right)^2-6xy+9\)
=> \(S^2-2P=P^2-6P+9\)
<=> \(S^2-\left(P-2\right)^2=5\)
<=> \(\left(S-P+2\right)\left(S+P-2\right)=5\)
TH1: \(\hept{\begin{cases}S-P+2=5\\S+P-2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}S-P=3\\S+P=3\end{cases}\Leftrightarrow\hept{\begin{cases}S=3\\P=0\end{cases}}}\)
khi đó: \(\hept{\begin{cases}x+y=3\\xy=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3;y=0\\x=0;y=3\end{cases}}\)
TH2: \(\hept{\begin{cases}S-P+2=1\\S+P-2=5\end{cases}}\Leftrightarrow\hept{\begin{cases}S-P=-1\\S+P=7\end{cases}\Leftrightarrow\hept{\begin{cases}S=3\\P=4\end{cases}}}\)
khi đó: \(\hept{\begin{cases}x+y=3\\xy=4\end{cases}}\)<=> không tồn tại x; y nguyên
TH3: \(\hept{\begin{cases}S-P+2=-5\\S+P-2=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}S-P=-7\\S+P=1\end{cases}\Leftrightarrow\hept{\begin{cases}S=-3\\P=4\end{cases}}}\)
khi đó: \(\hept{\begin{cases}x+y=-3\\xy=4\end{cases}}\)<=> không tồn tại x; y nguyên
TH4: \(\hept{\begin{cases}S-P+2=-1\\S+P-2=-5\end{cases}}\Leftrightarrow\hept{\begin{cases}S-P=-3\\S+P=-3\end{cases}\Leftrightarrow\hept{\begin{cases}S=-3\\P=0\end{cases}}}\)
Khi đó: \(\hept{\begin{cases}x+y=-3\\xy=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-3;y=0\\x=0;y=-3\end{cases}}\)
Vậy có 4 nghiệm nguyên ( 3; 0) ( -3: 0) ( 0; 3) ( 0; -3)