Những số nào sau đây chia cho 8 dư 1?
8.n (với n ∈ ℕ)
8.n + 1 (với n ∈ ℕ)
8.n - 1 (với n ∈ ℕ*)
8.(n + 1) (với n ∈ ℕ)
8.(n + 1) + 1 (với n ∈ ℕ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 9 2020
xời dăm ba cái bài này tui...........................ko thik làm
25 tháng 9 2020
+ Ta có: \(6n⋮6\forall n\)\(\Rightarrow\)\(6n+3:6\)dư \(3\)
\(6n-3:6\)dư \(6-3=3\)
+ Ta lại có: \(6.\left(n+3\right)⋮6\forall n\)\(\Rightarrow\)\(6.\left(n+3\right)+3:6\)dư \(3\)
Vậy \(6n+3,\)\(6n-3,\)\(6.\left(n+3\right)+3\)chia 6 dư 3
HH
1
NQ
6
HT
3
CM
21 tháng 5 2017
Chọn C
Áp dụng công thức khai triển nhị thức Newton:
Chọn x = -1 ta có 
17 tháng 6 2015
Số liền trước bằng số liền sau trừ 1
nên số liền trước của 3n +1 là 3n + 1 - 1 = 3n
17 tháng 6 2015
Dựa vào lý thuyết số liền trước kém số liền sau 1 đơn vị
nên số liền trước của số 3n+1 là 3n+1-1=3n+0=3n
CM
21 tháng 9 2017
Chọn A
Ta có 
Ta có 
Đạo hàm hai vế ta được: 
Đạo hàm 2 vế ta được: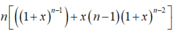 
Thay x = 1 vào 2 vế : 
Với n = 10, T =
1
2
C
n
1
+
2
2
C
n
2
+
.
.
.
.
+
n
2
C
n
n
CM
16 tháng 3 2019
Đáp án A
Ta có: ( − 1 ) 2 n + 1 = − 1 , ∀ n ∈ ℕ * nên A = {-1}
Vậy A chỉ có 1 phần tử
Số chia 8 dư 1 có dạng 8x + 1 (với x thuộc N)
Xét từng đáp án:
8n \(⋮\)8 (loại) (n thuộc N)
8n + 1 (chọn) (...)
8n - 1 = 8n + 8 - 7 = 8.(n + 1) - 7 chia 8 dư 7 (loại) (...)
8.(n + 1) \(⋮\)8 (loại) (...)
8.(n + 1) + 1 chia 8 dư 1 (chọn) (...)
Vì 8.(n + 1) \(⋮\)8 và 1 chia 8 dư 1
Vậy có 8n + 1 và 8.(n + 1) + 1 thỏa mãn đề bài