Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(A=\left\{x\in N|\left(2x+6\right)\left(x-3\right)=0\right\}\)
Mà: \(x\in N^+\)
\(\Rightarrow\left(2x+6\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+6=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-6\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\left(ktm\right)\\x=3\left(tm\right)\end{matrix}\right.\)
Vậy tập hợp A là:
\(A=\left\{3\right\}\)
Số phần từ là 1
⇒ Chọn B

Ta có:
\(A=\left\{x\in N|x⋮3;3\le x< 15\right\}\)
\(\Rightarrow A=\left\{3;6;9;12\right\}\)
Có số phần tử là 4
⇒ Chọn B

Ta có A = a = 3 n | n ∈ N * = 3 ; 6 ; 9 ; 12 ; ...
B = b ∈ N | 0 < b ≤ 9 = 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9
Ta thấy; 2 ∈ B ; 2 ∉ A nên B không thể là tập con của A.
Khẳng định B sai.
Đáp án B


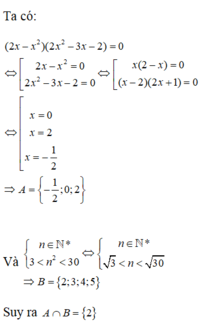
Đáp án A
Ta có: ( − 1 ) 2 n + 1 = − 1 , ∀ n ∈ ℕ * nên A = {-1}
Vậy A chỉ có 1 phần tử