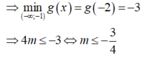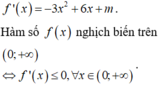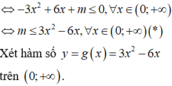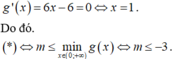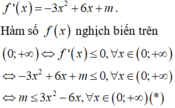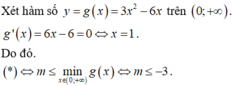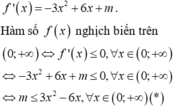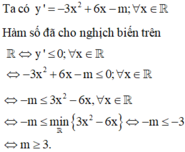Tìm m để y = x3 + 3x2 + (m+1)x + 4m nghịch biến trên (-1,1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NP
Nguyễn Phương Thảo
9 tháng 8 2020
Đúng(0)
Những câu hỏi liên quan
CM
8 tháng 10 2017
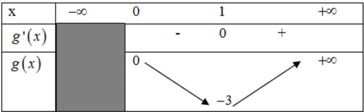
Ta có y ' = - 3 x 2 + 6 x + 3 m . Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình - 3 x 2 + 6 x + 3 m . Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1 khi đó, - 3 x 2 + 6 x + 3 m < 0 nên hàm số nghịch biến trên R .
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
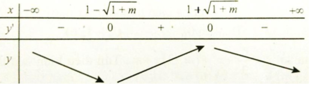
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y ' = - 3 x 2 + 6 x + 3 m ≤ 0 , ∀x > 0 <=> 3 m ≤ 3 x 2 - 6 x , ∀x > 0
Từ đó suy ra 3 m ≤ m i n ( 3 x 2 - 6 x ) với x > 0
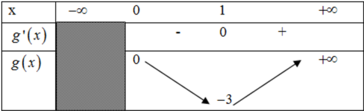
Mà 3 x 2 - 6 x = 3 ( x 2 - 2 x + 1 ) - 3 = 3 ( x - 1 ) 2 - 3 ≥ - 3 ∀ x
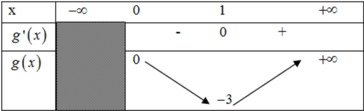
Suy ra: m i n ( 3 x 2 – 6 x ) = - 3 khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1.
Chọn đáp án C.
CM
30 tháng 5 2018
Tập xác định: D = R
y ' = 3 x 2 + 6 x + m có ∆ ' = 9 - 3 m
Nếu m ≥ 3 thì y ' ≥ 0 hàm số đồng biến trên R(loại)
Nếu m < 3 thì có 2 nghiệm phân biệt x 1 , x 2 x 1 < x 2
Hàm số nghịch biến trên đoạn x 1 ; x 2 với độ dài l = x 1 - x 2 .
Ta có x 1 + x 2 = - 2 ; x 1 x 2 = m 3 . Yêu cầu bài toán
⇔ x 1 + x 2 2 - 4 x 1 x 2 = 1 ⇔ x = 9 4
Đáp án B
CM
3 tháng 11 2017
Đáp án C
Phương pháp:
Hàm số y = f(x) nghịch biến trên D khi và chỉ khi 
và bằng 0 tại hữu hạn điểm
Cách giải:
Ta có: 
Hàm số đã cho nghịch biến trên 
Xét hàm số: 
ta có: 
