△ ABC , Â = 90o, đường cao AH , trung tuyến AM . Kẻ HE ⊥ AB , HF ⊥ AC .
a) Chứng minh rằng : AE . AB = AF . AC .
b) Chứng minh rằng : AM ⊥ EF .
c) Cho BC cố định , xác định A để EF max .
d) Cho BC cố định , xác định A để SAEHF max .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 10 2021
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{EAF}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=EF
12 tháng 11 2021
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=FE
AH
Akai Haruma
Giáo viên
3 tháng 5 2018
Lời giải:
Bạn tự vẽ hình nhé.
a) Ta thấy \(\widehat{MFC}=90^0-\widehat{MAF}(1)\)
VÌ $AM$ là trung tuyến ứng với cạnh huyền nên \(AM=\frac{BC}{2}=BM=MC\)
\(\Rightarrow \triangle AMB\) cân tại $M$
\(\Rightarrow \widehat{MBE}=\widehat{MBA}=\widehat{MAB}=90^0-\widehat{MAF}(2)\)
Từ \((1);(2)\Rightarrow \widehat{MFC}=\widehat{MBE}\)
Xét tam giác $MBE$ và $MFC$ có:
\(\left\{\begin{matrix} \widehat{MBE}=\widehat{MFC}\\ \widehat{BME}=\widehat{FMC}(\text{đối đỉnh})\end{matrix}\right.\) \(\Rightarrow \triangle MBE\sim \triangle MFC(g.g)\)
b) Theo phần a thì \(\widehat{MBE}=\widehat{MFC}\Leftrightarrow \widehat{ABC}=\widehat{AFE}\)
Xét tam giác $ABC$ và $AFE$ có:
\(\left\{\begin{matrix} \widehat{ABC}=\widehat{AFE}\\ \text{chung góc A}\end{matrix}\right.\Rightarrow \triangle ABC\sim \triangle AFE(g.g)\)
\(\Rightarrow \frac{AB}{AF}=\frac{AC}{AE}\Rightarrow AB.AE=AC.AF\)
c)
Do $AH,AM$ là hai đường cao tương ứng đỉnh $A$ của hai tam giác đồng dạng $ABC$ và $AFE$ nên \(\frac{AH}{AM}=\frac{AB}{AF}=\frac{AC}{AE}\)
Do đó \(\frac{S_{ABC}}{S_{AEF}}=\frac{\frac{AB.AC}{2}}{\frac{AE.AF}{2}}=\frac{AB}{AF}.\frac{AC}{AE}=\left(\frac{AH}{AM}\right)^2(*)\)
Xét tam giác $AMI$ và $AHM$ có:
\(\left\{\begin{matrix} \text{chung góc A}\\ \widehat{AMI}=\widehat{AHM}=90^0\end{matrix}\right.\Rightarrow \triangle AMI\sim \triangle AHM(g.g)\)
\(\Rightarrow \frac{AM}{AI}=\frac{AH}{AM}(**)\)
Từ \((*);(**)\Rightarrow \frac{S_{ABC}}{S_{AEF}}=\left(\frac{AM}{AI}\right)^2\) (đpcm)
Q
1 tháng 8 2017
a) Gọi G là trung điểm của EC.
Xét ΔBEC có: EG = CG (cách vẽ); BM = CM (gt).
=> MG là đường trung bình của ΔBEC.
=> MG // BE hay MG // DE.
Ta có: \(AE+EG+GC=AC\)
mà \(AE=\dfrac{1}{3}AC\) (1)
=> \(EG+GC=\dfrac{2}{3}AC\)
lại có: EG = GC (cách vẽ).
=> \(EG=GC=\dfrac{1}{3}AC\) (2)
Từ (1) và (2) suy ra AE = EG = GC.
Xét ΔAMG có: MG // DE (cmt); AE = EG (cmt).
=> AD = MD.
b) Lấy H là trung điểm của BF.
Áp dụng định lý Ta-lét, ta có: \(AF:FH:HB=AE:EG:GC\)
mà AE = EG = GC (câu a).
=> AF = FH = HB.
Xét ΔAHG có: AE = GE (cm ở câu a); AF = FH (cmt).
=> EF là đường trung bình của ΔAHG.
=> EF // HG.
tương tự nếu cm đc HG // BC thì bắc cầu lại EF // BC.
23 tháng 5 2022
a: Gọi K là trung điểm của EC
=>AE=EK=KC
Xét ΔBEC có
M là trung điểm của BC
K là trung điểm của EC
Do đó: MK là đường trung bình
=>MK//BE và MK=BE/2
Xét ΔAMK có
E là trung điểm của AK
ED//MK
Do đó: D là trung điểm của AM
b: Gọi G là trung điểm của FB
Xét ΔBFC có
G là trung điểm của BF
M là trung điểm của BC
Do đó: GM là đường trung bình
=>GM//FC
hay FD//GM
Xét ΔAGM có
D là trung điểm của AM
DF//GM
Do đó: F là trung điểm của AG
=>AF=FG=GB
=>AF=1/3AB
Xé ΔABC có AF/AB=AE/AC
nên FE//BC
L
14 tháng 12 2021
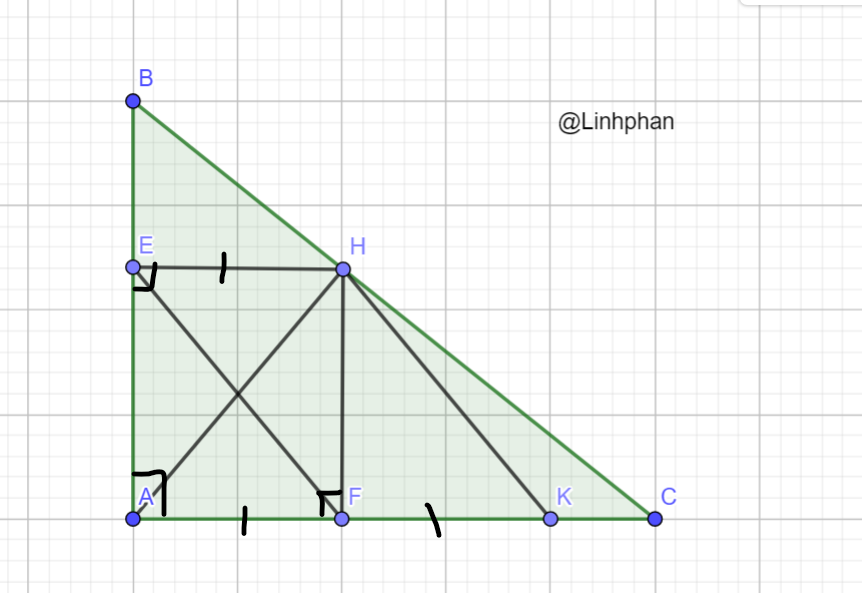
a, Vì HE ⊥ AB ; FA ⊥ AB => HE // FA (từ ⊥ đến // )
+, EA ⊥ AC ; HF ⊥ AC => EA // HF (từ ⊥ đến // )
Xét tứ giác AEHF có: HE // FA (cmt) ; EA // HF (cmt)
=> Tứ giác AEHF là hình bình hành (dhnb)
mà \(\hat{EAF} =90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> AH = EF
b, Vì AEHF là hình chữ nhật (cmt)
=> EH//AF; EH = AF mà AF= FK (gt)
=> EH = FK
+, Xét tứ giác EHKF có: EH = FK (cmt)
EH // FK (do EH // AF; K ∈ AF)
=> Tứ giác EHKF là hình bình hành (dhnb)
a) Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh AB(gt)
nên \(AH^2=AE\cdot AB\)(định lí 1 về hệ thức lượng trong tam giác vuông)(1)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh AC(gt)
nên \(AF\cdot AC=AH^2\)(định lí 1 về hệ thức lượng trong tam giác vuông)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)(đpcm)
b) Ta có: \(AE\cdot AB=AF\cdot AC\)(cmt)
\(\Rightarrow\frac{AE}{AC}=\frac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\frac{AE}{AC}=\frac{AF}{AB}\)(cmt)
Do đó: ΔAEF∼ΔACB(c-g-c)
⇒\(\widehat{AEF}=\widehat{ACB}\)(3)
Xét ΔABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC(gt)
nên \(AM=\frac{BC}{2}\)(định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CM=\frac{BC}{2}\)(M là trung điểm của BC)
nên AM=CM
Xét ΔAMC có AM=CM(cmt)
nên ΔAMC cân tại M(định nghĩa tam giác cân)
⇒\(\widehat{C}=\widehat{MAC}\)(hai góc ở đáy)(4)
Từ (3) và (4) suy ra \(\widehat{AEF}=\widehat{MAC}\)
Xét ΔAFE vuông tại A có \(\widehat{AFE}+\widehat{AEF}=90^0\)(hai góc nhọn phụ nhau)
mà \(\widehat{AEF}=\widehat{MAC}\)(cmt)
nên \(\widehat{AFE}+\widehat{MAC}=90^0\)
hay \(\widehat{AFI}+\widehat{IAF}=90^0\)
Xét ΔAIF có \(\widehat{AFI}+\widehat{IAF}=90^0\)(cmt)
nên ΔAIF vuông tại I(định lí đảo của tam giác vuông)
⇒IA⊥IF
hay AM⊥EF(đpcm)