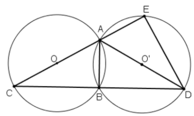
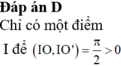Cho hai đường tròn bằng nhau (O;R) và (O';R) cắt nhau tại A và B sao cho AB=R. Kẻ đk AC của đường tròn tâm (O). Gọi E là một điểm bất kì thuộc cung nhỏ BC. CB và EB lần lượt cắt (O') tại các điểm thứ 2 là D và F
a) CM \(\widehat{AFD}=90\) độ
b) CM AE=AF
c) Gọi P là giao điểm của CE và FD. Cm AP là đường trung trực của EF
d) Tính tỉ số \(\frac{AQ}{AP}\)

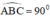
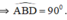
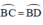 ( định lý )
( định lý )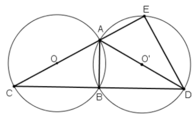
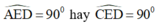
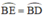 (định lý) hay B là điểm chính giữa cung
(định lý) hay B là điểm chính giữa cung 
 có số đo bằng nhau.
có số đo bằng nhau.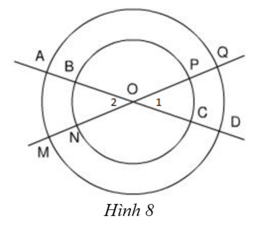
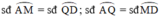
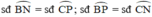
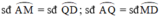
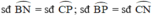
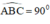
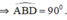
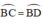 ( định lý )
( định lý )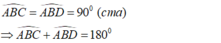
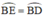 (định lý) hay B là điểm chính giữa cung
(định lý) hay B là điểm chính giữa cung