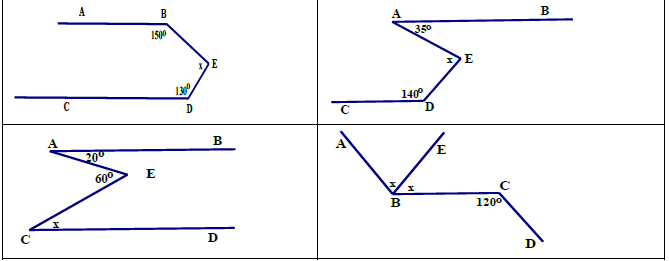
Bài 1: Tìm số đo x trong các hình sau, biết AB//CD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bafi1: Do AB // CD ( GT )
⇒ˆA+ˆC=180o
⇒2ˆC+ˆC=180o
⇒3ˆC=180o
⇒ˆC=60o
⇒ˆA=60o.2=120o
Do ABCD là hình thang cân
⇒ˆC=ˆD
Mà ˆC=60o
⇒ˆD=60o
AB // CD ⇒ˆD+ˆB=180o
⇒ˆB=180o−60o=120o
Vậy ˆA=ˆB=120o;ˆC=ˆD=60o
Bài 2:
Ta có; AB//CD
\(\Rightarrow\)góc BAD+ góc ADC= \(180^o\)
^A=3. ^D \(\Rightarrow\)\(\dfrac{A}{3}\)=^D
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{A}{3}=\dfrac{D}{1}=\dfrac{A+D}{3+1}=\dfrac{180^O}{4}=45^O\)
\(\Rightarrow\)^A= \(135^O\)
\(\Rightarrow\)^D=\(45^o\)
\(\Rightarrow B=A=135^o\)
\(\Rightarrow C=D=45^o\)

a) Ta kẻ đường thẳng đi qua E song song với AB và CD, ta dễ dàng tính được E C D ^ = 30 ° .
b) Ta kẻ đường thẳng đi qua E song song với AB và CD, dễ dàng tính được E ^ = 30 ° + 45 ° = 75 °

a) A+B+C=180 độ (tổng ba góc của tam giác)
90 độ +55 độ + x=180 đ
145 độ +x=180
x=180-145
x=35

a. B C ⊥ A B B C ⊥ C D ⇒ A B / / C D
b. A D C ^ + D A B ^ = 180 ° ( trong cùng phìa)
⇒ A D C ^ = 40 °

Có \(\widehat{CMA}+\widehat{CMB}=180^0\) (Hai góc kề bù)
\(\Leftrightarrow5\widehat{CMA}+\widehat{CMA}=180^0\Leftrightarrow\widehat{CMA}=30^0\)
\(\Rightarrow\widehat{BMC}=5.30^0=150^0\)
Có \(\widehat{CMA}+\widehat{AMD}=180^0\)
\(\Leftrightarrow\widehat{AMD}=180^0-30^0=150^0\)
Có \(\widehat{DMB}=\widehat{AMC}=150^0\) (Hai góc đối đỉnh)
Vậy...
\(x=80^o\) \(x=75^o\)
\(x=20^o\) \(x=60^o\)
chi tiết