hệ phương trình y=4x-23 và x=3(y+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
RN
0
CM
29 tháng 1 2018
Bài toán này có hai cách giải:
Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.
Cách 2: Đặt ẩn phụ.
Cách 1:
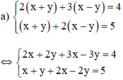
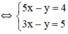(hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)
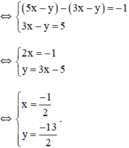
Vậy hệ phương trình có nghiệm duy nhất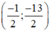 
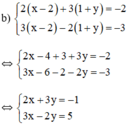
(Nhân hai vế pt 1 với 2; pt 2 với 3 để hệ số của y đối nhau)
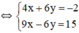(Hệ số của y đối nhau nên ta cộng từng vế của hai pt)
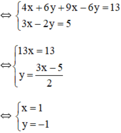
Vậy hệ phương trình có nghiệm duy nhất (1; -1).
Cách 2:
a) Đặt x + y = u và x – y = v (*)
Khi đó hệ phương trình trở thành
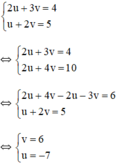
Thay u = -7 và v = 6 vào (*) ta được hệ phương trình:
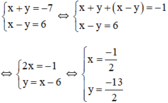
Vậy hệ phương trình có nghiệm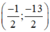 
b) Đặt x – 2 = u và y + 1 = v.
Khi đó hệ phương trình trở thành :
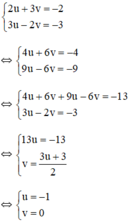
+ u = -1 ⇒ x – 2 = -1 ⇒ x = 1.
+ v = 0 ⇒ y + 1 = 0 ⇒ y = -1.
Vậy hệ phương trình có nghiệm (1; -1).
TN
0
CM
24 tháng 9 2017
ĐK: y − 2 x + 1 ≥ 0 , 4 x + y + 5 ≥ 0 , x + 2 y − 2 ≥ 0 , x ≤ 1
T H 1 : y − 2 x + 1 = 0 3 − 3 x = 0 ⇔ x = 1 y = 1 ⇒ 0 = 0 − 1 = 10 − 1 ( k o t / m ) T H 2 : x ≠ 1 , y ≠ 1
Đưa pt thứ nhất về dạng tích ta được
( x + y − 2 ) ( 2 x − y − 1 ) = x + y − 2 y − 2 x + 1 + 3 − 3 x ( x + y − 2 ) 1 y − 2 x + 1 + 3 − 3 x + y − 2 x + 1 = 0 ⇒ 1 y − 2 x + 1 + 3 − 3 x + y − 2 x + 1 > 0 ⇒ x + y − 2 = 0
Thay y= 2-x vào pt thứ 2 ta được x 2 + x − 3 = 3 x + 7 − 2 − x
⇔ x 2 + x − 2 = 3 x + 7 − 1 + 2 − 2 − x ⇔ ( x + 2 ) ( x − 1 ) = 3 x + 6 3 x + 7 + 1 + 2 + x 2 + 2 − x ⇔ ( x + 2 ) 3 3 x + 7 + 1 + 1 2 + 2 − x + 1 − x = 0
Do x ≤ 1 ⇒ 3 3 x + 7 + 1 + 1 2 + 2 − x + 1 − x > 0
Vậy x + 2 = 0 ⇔ x = − 2 ⇒ y = 4 (t/m)
\(\hept{\begin{cases}y=4x-23\\x=3\left(y+1\right)\end{cases}}\Leftrightarrow\hept{\begin{cases}y=4x-23\left(k\right)\\x=3y+3\left(h\right)\end{cases}}\)
Thay x vào k ta đc
\(y=4\left(3y+3\right)-23\)
\(\Leftrightarrow y=12y+12-23\Leftrightarrow-11y=-11\Leftrightarrow y=1\)
Thay y = 1 vào h ta đc
\(x=3.1+3\Leftrightarrow x=6\)