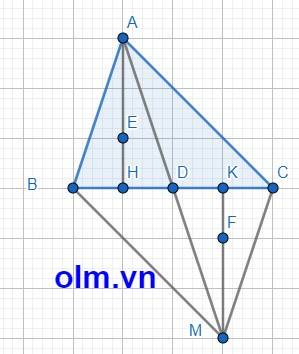
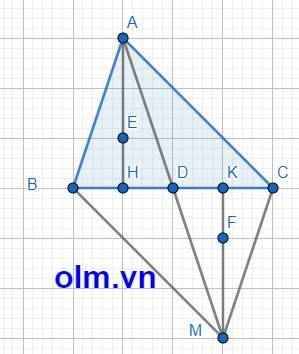
+ Cho tam giác ABC, trên cạnh AC lấy điểm M sao cho ABM = ACB. Từ A kẻ AH vuông góc với BC (H thuộc BC), AK vuông góc với BM (K thuộc BM).
a) Chứng minh tam giác ABM đồng dạng với tam giác ACB.
b) Chứng minh: AB.AK = AM.AH.
c) Chứng minh: Diện tích tam giác AHB gấp 4 lần diện tích tam giác AKM (biết AB = 3cm, AC = 6cm).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 1 2022
a) \(\Delta ABC\) cân tại A (gt).
\(\Rightarrow\left\{{}\begin{matrix}AB=AC\\\widehat{ABC}=\widehat{ACB}\end{matrix}\right.\) (Tính chất tam giác cân).
Mà \(\widehat{ABC}+\widehat{ABM}=180^o;\widehat{ACB}+\widehat{ACN}=180^o.\)
\(\Rightarrow\widehat{ABM}=\widehat{ACN}.\)
Xét \(\Delta ABM\) và \(\Delta ACN:\)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right).\\ MB=CN\left(gt\right).\\ AB=AC\left(cmt\right).\)
\(\Rightarrow\) \(\Delta ABM\) \(=\) \(\Delta ACN\left(c-g-c\right).\)
b) Xét \(\Delta ABH\) và \(\Delta ACK:\)
\(AB=AC\left(cmt\right).\\ \widehat{AHB}=\widehat{AKC}\left(=90^o\right).\\ \widehat{HAB}=\widehat{KAC}\left(\Delta ABM=\Delta ACN\right).\)
\(\Rightarrow\Delta ABH=\Delta ACK\) (cạnh huyền - góc nhọn).
\(\Rightarrow\) AH = AK (2 cạnh tương ứng).
c) Xét \(\Delta AOH\) và \(\Delta AOK:\)
\(AH=AK\left(cmt\right).\\ AOchung.\\ \widehat{AHO}=\widehat{AKO}\left(=90^o\right).\)
\(\Rightarrow\) \(\Delta AOH\) \(=\) \(\Delta AOK\) (cạnh huyền - cạnh góc vuông).
\(\Rightarrow\) OH = OK (2 cạnh tương ứng).
Mà \(\left\{{}\begin{matrix}OB=OH-HB;OC=OK-KC.\\HB=KC\left(\Delta ABH=\Delta ACK\right).\end{matrix}\right.\)
\(\Rightarrow\) OB = OC.
\(\Rightarrow\Delta OBC\) cân tại O.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 1
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
K
7 tháng 1
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .
20 tháng 6 2020
a) Xét ΔABMΔABM và ΔACBΔACB có:
ˆAA^ chung
ˆABM=ˆACBABM^=ACB^
Do đó ΔABMΔABM ∽ ΔACBΔACB (g - g)
b) Vì ΔABMΔABM ∽ ΔACBΔACB (cmt)
và ABAC=AMABABAC=AMAB (Đ/n hai tam giác đồng dạng)
⇒AM=AB2AC=224=1(cm)⇒AM=AB2AC=224=1(cm)
c) Vì ΔABMΔABM ∽ ΔACBΔACB (cmt)
⇒ˆAMB=ˆABC⇒AMB^=ABC^
⇒ˆAMK=ˆABH⇒AMK^=ABH^
Xét ΔAHBΔAHB và ΔAKMΔAKM có:
ˆAHB=ˆAKM=900AHB^=AKM^=900 (Vì AH⊥BC,AK⊥BMAH⊥BC,AK⊥BM
ˆABH=ˆAMKABH^=AMK^ (cmt)
Do đó ΔAHBΔAHB ∽ ΔAKMΔAKM (g - g)
Suy ra AHAK=ABAMAHAK=ABAM
⇒AH.AM=AB.AK⇒AH.AM=AB.AK (đpcm)
6 tháng 1 2023
a, Xét tam giác `ADC` và tam giác `MDB` có:
`DB=DC` `(g``t)`
\(\widehat{MDB}=\widehat{ADC}\) (2 góc đối đỉnh)
`DM=DA` `(g``t)`
`=>` Tam giác `ADC=` `MDB` `(c-``g-``c)`
`b,` vì tam giác `ADC=` Tam giác `MDB` (theo a)
`=> AC = BM` (2 cạnh tương ứng)
`=>` \(\widehat{ACD}=\widehat{MBD}\) (2 góc tương ứng)
mà 2 góc này nằm ở vị trí sole trong
`=> AC` //`BM` (d. hiệu nhận biết) (đpcm)
c, Vì Tam giác `ADC=` Tam giác `MDB` (theo a)
`=>`\(\widehat{DAC}=\widehat{DMB}\) (2 góc tương ứng)
Xét Tam giác `ABM` và Tam giác `MCA` có:
AM chung
\(\widehat{DAC}=\widehat{DMB}\) `(CMT)`
`BM = AC (CMT)`
`=>` Tam giác `ABM =` Tam giác `MCA (c-g-c)
d, *xl cậu câu này mình bí mất r:')
12 tháng 7 2023
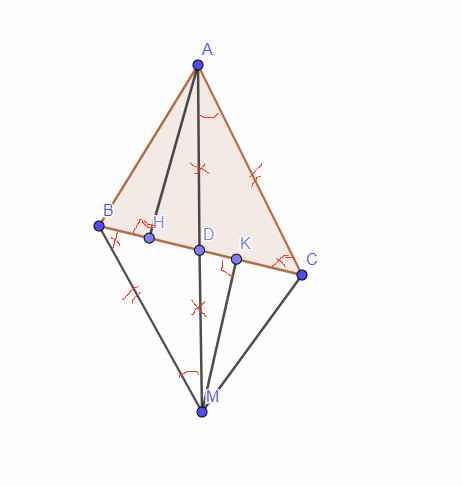
a: Xét ΔBAM có BA=BM và góc ABM=60 độ
nên ΔBAM đều
b: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
=>góc BMD=góc BAD=90 độ
=>DM vuông góc BC
26 tháng 2 2021
a) Xét ΔABC có
BC>AB(15cm>7cm)
mà góc đối diện với cạnh BC là \(\widehat{BAC}\)
và góc đối diện với cạnh AB là \(\widehat{ACB}\)
nên \(\widehat{BAC}>\widehat{ACB}\)(Định lí quan hệ giữa cạnh và góc đối diện trong tam giác)
CHO TUI LỜI GIẢI OK BN