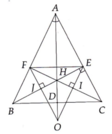
Cho Δ ABC, ba đường cao BE, BF và AD cắt nhau tại H. Từ E kẻ EI ⊥ AD tại I. Qua A kẻ đường thẳng d song song với BC. Gọi J là giao của CI và d. Chứng minh D,F,J thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

24 tháng 6 2023
a: Xét ΔABH và ΔACH có
AB=AC
góc BAH=góc CAH
AH chung
=>ΔABH=ΔACH
=>BH=CH
b: Xét ΔEAH và ΔECF có
góc EAH=góc ECF
EA=EC
góc AEH=góc CEF
=>ΔEAH=ΔECF
=>EH=EF

15 tháng 1 2022
a. Xét tam giác ABC có:
DE//BC (gt)
=>\(\dfrac{DA}{DB}=\dfrac{EA}{EC}\)(định lý Ta-let) (1)
Xét tam giác ADE có:
AD//CF (gt)
=>\(\dfrac{EA}{EC}=\dfrac{DE}{EF}\)(định lý Ta-let) (2)
Từ (1) và (2) suy ra:\(\dfrac{DA}{DB}=\dfrac{ED}{FE}\)

12 tháng 5 2023
a: Xét ΔBAH và ΔBDH có
BA=BD
AH=DH
BH chung
=>ΔBAH=ΔBDH
b: Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>DA=DE