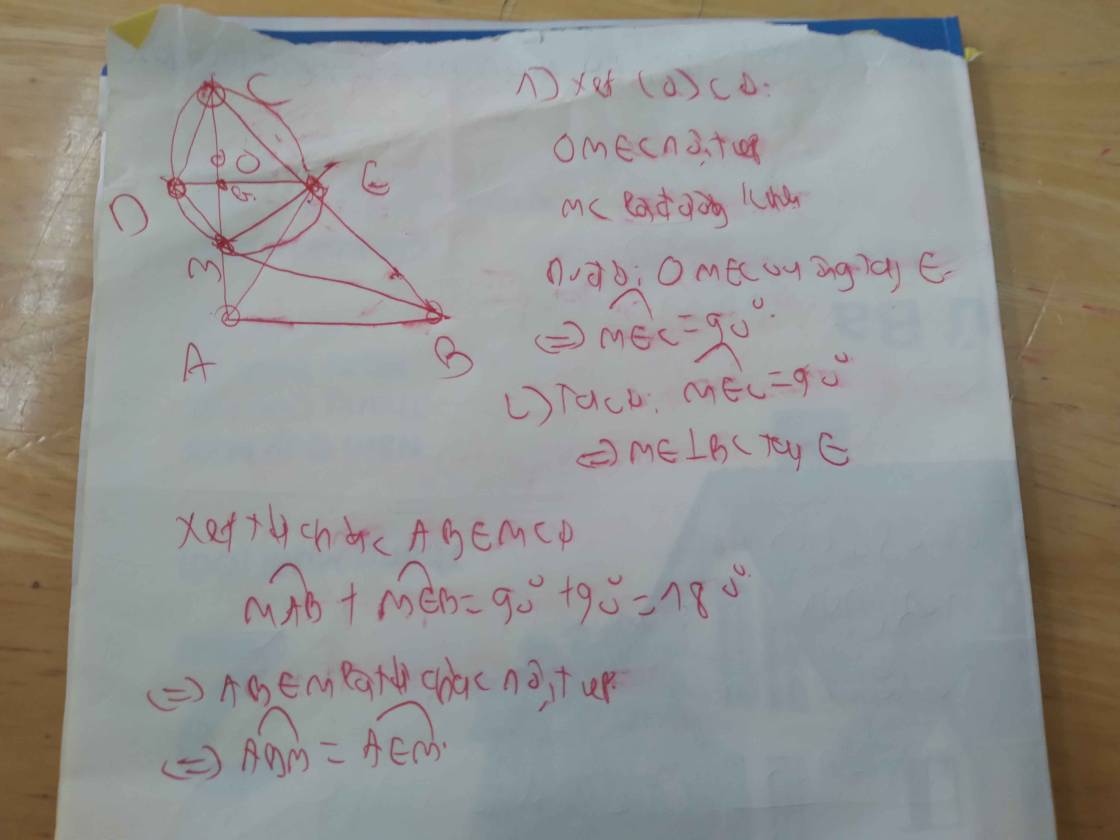
Cho tam giác ABC vuông tại B. Trên cạnh BC lấy điểm E( E khác B và C) . Đường tròn đường kính EC cắt cạnh AC tại M và cắt đường thẳng AE tại N( M khác C, N, khác E).
a) chứng minh ABEM và ABNC là tứ giác nội tiếp
b) chứng minh ME là tia phân giác của góc BMN
C) chứng minh AE.AN + CE.CB= AC2
Cho mk hỏi phần b,c với ạ mk cảm ơn !