Cho hai đường tròn (O;R) và (O'; r) cắt nhau tại hai điểm A và B. Biết OO' = \(2+2\sqrt{3}\) (cm); góc AOB = 600; góc AO'B = 900. Tính bán kính R, r
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có: góc ABC = 90 độ ( góc nt chắn nửa đt )
góc ABD = 90 độ ( góc nt chắn nửa đt )
=> CBD = góc ABC + góc ABD = 180 độ
=> ba điểm C,B,D thẳng hàng
hình bẹn tự vẽ hén:
giải:
Có \(\widehat{ABC}=90^o\) ( vì góc ABC chắn nửa đường tròn đường kính AC)
\(\widehat{ABD}=90^o\) ( vì góc ABD chắn nửa đường tròn đường kính AD)
\(\Rightarrow\widehat{ABC}+\widehat{ABD}=180^o\)
Vậy ba điểm C; B ; D thẳng hàng.

Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A'B' của hai đường tròn (o),(O') cắt nhau tại P(A và A' thuộc đường tròn (O'), B và B' thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O').
Hướng dẫn làm bài:
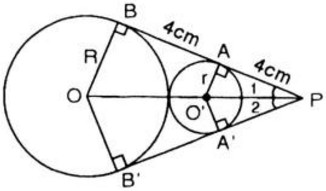
Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
ˆA=ˆB=900A^=B^=900
ˆP1P1^ chung
Vậy ΔOBP ~ ∆ O’AP
⇒rR=PO′PO=PAPB=48=12⇒R=2r⇒rR=PO′PO=PAPB=48=12⇒R=2r
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)

Vì AB là tiếp tuyến chung của (O) và (O’) nên OB ⊥ AB và O’A ⊥ AB
Xét hai tam giác vuông OPB và O’AP, ta có:
ˆA=ˆB=900A^=B^=900
ˆP1P1^ chung
Vậy ΔOBP ~ ∆ O’AP
⇒rR=PO′PO=PAPB=48=12⇒R=2r⇒rR=PO′PO=PAPB=48=12⇒R=2r
Ta có PO’ = OO’ = R + r = 3r (do AO’ là đường trung bình của ∆OBP)
Áp dụng định lí Py-ta-go trong tam giác vuông O’AP
O’P = O’A2 + AP2 hay (3r)2 = r2 + 42 ⇔ 9r2 = r2 + 16 ⇔ 8 r2 =16 ⇔ r2 = 2
Diện tích đường tròn (O’;r) là: S = π. r2 = π.2 = 2π (cm2)

c: góc BDC=1/2*góc BOC=60 độ
BD//AC
=>góc DCx=góc BDC=60 độ(so le trong)
=>góc ODC=góc OCD=90-60=30 độ
góc BDO=góc CDO=30 độ
=>góc BOD=góc COD=120 độ
=>ΔBOD=ΔCOD
=>BD=CD
=>D nằm trên trung trực của BC
=>A,O,D thẳng hàng

a) Áp dụng định lý Py-ta-go, ta tính được AB = 4(cm)
(câu a tự trình bày nhé)
b) Gọi H= OA _|_ BC . khi đó H là trung điểm BC
=> HB = HC
Xét 2 tam giác vuông AHB và AHC:
AH chung; HB = HC (cmt)
=> tam giác AHB = tam giác AHC (2 cạnh góc vuông)
=> ABH^ = ACH^
Mặt khác, OBC^ = OCB^ (tam giác BOC cân tại O, OB=R=OC)
Mà OBC^ + ABH^ = 90o (Ax là tiếp tuyến)
=> OCB^ + ACH^ = 90o => ACO^ = 90o => AC là tiếp tuyến (O)
c) Xét tam giác BCD:
CD là đường kính (gt) => O là trung điểm CD
Mà H là trung điểm BC (cmt)
=> OH là đường trung bình của tam giác BCD
=> OH // BD hay OA // BD

Δ
a: Xét ΔOAM vuông tại A có cos AOM=OA/OM=1/2
nên góc AOM=60 độ
=>góc AMO=30 độ
Xét ΔOAC có OA=OC và góc AOM=60 độ
nên ΔAOC đều
mà AH là đường cao
nên H là trung điểm của OC
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
Xét tứ giác OACB có
H là trung điểm chung của OC và BA
OA=OB
Do đó: OACB là hình thoi
b: góc DAM=180 độ-góc HAM=180-60=120 độ
góc DAO=180-60=120 độ
góc OAM=360-120-120=120 độ
=>góc DAM=góc DAO=góc OAM
=>ΔODM đều
=>MO=MD
=>M nằm trên trung trực của OD
mà NK là trung trực của OD
nên M,N,K thẳng hàng
Ta có : Đường tròn tâm O cắt O, tại A và B .
=> OO, là đường trung trực của AB .
=> \(\left\{{}\begin{matrix}HA=HB=\frac{1}{2}AB\\AB\perp OO^,\end{matrix}\right.\)
=> \(\widehat{AO^,H}=\frac{1}{2}\widehat{AO^,B}=45^o\)
Mà tam giác AHO, vuông .
=> Tam giác AHO, vuông cân .
- Áp dụng định lý pi ta go vào tam giác AHO, có :
\(AO^,=\sqrt{AH^2+OH^{,2}}=\sqrt{2AH^2}=\sqrt{2\left(\frac{AB}{2}\right)^2}=\sqrt{\frac{AB^2}{2}}\)
- Áp dụng định lý pi ta go vào tam giác AHO, có :
\(O^,H=\sqrt{AO^{,2}-AH^2}=\sqrt{\frac{AB^2}{2}-\left(\frac{AB}{2}\right)^2}=\sqrt{\frac{AB^2}{4}}=\frac{AB}{2}\)
- Áp dụng định lý pi ta go vào tam giác AHO có :
\(OH=\sqrt{AO^2-AH^2}\)
Mà tam giác OAB là tam giác đều ( \(\left\{{}\begin{matrix}OA=OB=R\\\widehat{AOB}=60^o\end{matrix}\right.\) )
=> \(AO=AB\)
=> \(OH=\sqrt{AB^2-\left(\frac{AB}{2}\right)^2}=\sqrt{\frac{3AB^2}{4}}=\frac{AB\sqrt{3}}{2}\)
Ta có : \(OO^,=OH+O^,H=\frac{AB}{2}+\frac{AB\sqrt{3}}{2}=2+2\sqrt{3}\)
=> AB = 4 ( cm )
=> \(AH=BH=\frac{1}{2}AB=2\left(cm\right)\)
- Áp dụng tỉ số lượng giác vào :
\(\left\{{}\begin{matrix}\Delta AHO^,\perp H:SinAO^,H=Sin45=\frac{AH}{AO^,}=\frac{2}{AO^,}\\\Delta AHO\perp H:SinAOH=Sin30=\frac{AH}{AO}=\frac{2}{AO}\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}AO^,=2\sqrt{2}=r\\AO=4=R\end{matrix}\right.\) ( cm )