Giúp mình với..
Đề bài: Cho tam giác ABC ( góc A=90 độ), đường cao AH. Chứng minh rằng AH\(^2\)= BH.CH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 3 2023
3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)
PT
1
CM
21 tháng 8 2019
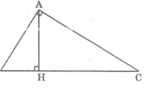
Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: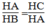 
Vậy A H 2 = B H . C H
9 tháng 5 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
MP
9 tháng 5 2023
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm
Xét \(\Delta\)ABH và \(\Delta\)CAH có:\(\widehat{AHB}=\widehat{AHC}=90^0;\widehat{BAH}=\widehat{HCA}\)
\(\Rightarrow\Delta ABH~\Delta CAH\left(g.g\right)\Rightarrow\frac{AH}{CH}=\frac{BH}{AH}\Rightarrow AH^2=BH\cdot CH\)
\(\Rightarrowđpcm\)