Trong mặt phẳng vớ hệ tọa độ Oxy, cho đường tròn (C): (x - 2)2 + (y - 1)2 = 25 và đường thẳng d: x - 2y + 15 = 0. Hình vuông ABCD ngoại tiếp đường tròn (C) và đỉnh A thuộc đưởng thẳng d. Tìm tọa độ đỉnh B của hình vuông biết rằng đỉnh A có hoành độ dương.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\widehat{AHC}=\widehat{AEC}=90^0\) nên 4 điểm A, H, C, E cùng thuộc đường tròn đường kính AC.
Gọi I là giao điểm của AC và BD
Ta có \(\widehat{HIE}=2\widehat{HAE}=2\left(180^0-\widehat{BCD}\right)\)
Các tứ giác AKED, AKHB nội tiếp nên \(\widehat{EKD}=\widehat{EAD}\) và \(\widehat{BKH}=\widehat{BAH}\)
Do đó \(\widehat{HKE}=180^0-\widehat{AKD}-\overrightarrow{BKH}=180^0-\overrightarrow{EAD}-\overrightarrow{BAH}=2\overrightarrow{HAE}=2\left(180^0-\overrightarrow{BCD}\right)=\overrightarrow{HIE}\)
Vậy tứ giác HKIE nội tiếp. Do đó I thuộc đường tròn (C) ngoại tiếp tam giác HKE
- Gọi \(C\left(c;c-3\right)\in d\left(c>0\right)\Rightarrow I\left(\frac{c-2}{2};\frac{c-4}{2}\right)\)
Do I thuộc (C) nên có phương trình :
\(c^2-c-2=0\Leftrightarrow c=2\) V c=-1 (loại c=-1) Suy ra \(C\left(2;-1\right);I\left(0;-1\right)\)
- Điểm E, H nằm trên đường tròn đường kính AC và đường tròn (C) nên tọa độ thỏa mãn hệ phương trình :
\(\begin{cases}x^2+y^2+x+4y+3=0\\x^2+\left(y+1\right)^2=4\end{cases}\) \(\Leftrightarrow\begin{cases}x=0;y=-3\\x=-\frac{8}{5};y=-\frac{11}{2}\end{cases}\)
- Vì H có hoành độ âm nên \(H\left(-\frac{8}{5};-\frac{11}{5}\right);E\left(0;-3\right)\) Suy ra \(AB:x-y+1=0;BC:x-3y-5=0\)
Tọa độ B thỏa mãn \(\begin{cases}x-y+1=0\\x-3y-5=0\end{cases}\) \(\Leftrightarrow B\left(-4;-3\right)\Rightarrow\overrightarrow{BA}=\left(2;2\right);\overrightarrow{BC}=\left(6;2\right)\Rightarrow\overrightarrow{BA}.\overrightarrow{BC}=16>0\)
Vì \(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow D\left(4;1\right)\)
Vậy \(B\left(-4;-3\right);C\left(2;-1\right);D\left(4;1\right)\)

Đáp án A
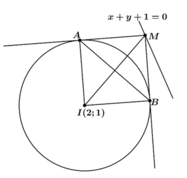
- Do M thuộc d suy ra M( t; -1-t).
Nếu 2 tiếp tuyến vuông góc với nhau thì MAIB là hình vuông
(A; B là 2 tiếp điểm).
Do đó:
![]()
- Ta có :
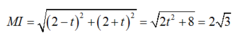
- Do đó : 2t2+ 8= 12
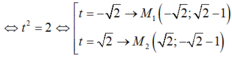

1.
\(\left(C\right):x^2+y^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)
Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)
Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)
Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)
\(\Leftrightarrow m=-1\pm\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)
2.
Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)
\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)


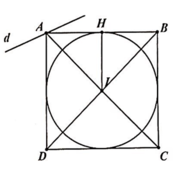



Đường tròn (C) tâm \(I\left(2;1\right)\) bán kính \(R=5\)
Hình vuông ngoại tiếp đường tròn \(\Rightarrow AB=2R=10\)
Gọi M là tiếp điểm của (C) và AB \(\Rightarrow\) M là trung điểm AB và \(IM=R=\frac{AB}{2}=5\) ; \(AM=\frac{AB}{2}=5\)
Do A thuộc d nên tọa độ có dạng: \(A\left(2a-15;a\right)\)
\(\Rightarrow\overrightarrow{IA}=\left(2a-17;a-1\right)\)
Áp dụng Pitago: \(AM^2+IM^2=IA^2\Rightarrow\left(2a-17\right)^2+\left(a-1\right)^2=50\)
\(\Leftrightarrow5a^2-70a+240=0\Rightarrow\left[{}\begin{matrix}a=6\\a=8\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}A\left(-3;6\right)\left(loại\right)\\A\left(1;8\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{AI}=\left(1;-7\right)\) \(\Rightarrow\) phương trình BI qua I và vuông góc AI có dạng:
\(1\left(x-2\right)-7\left(y-1\right)=0\Leftrightarrow x-7y+5=0\)
\(\Rightarrow B\left(7b-5;b\right)\Rightarrow\overrightarrow{IB}=\left(7b-7;b-1\right)\)
\(IB^2=IA^2=50\Rightarrow\left(7b-7\right)^2+\left(b-1\right)^2=50\)
\(\Leftrightarrow\left(b-1\right)^2=1\Rightarrow\left[{}\begin{matrix}b=0\\b=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}B\left(-5;0\right)\\B\left(9;2\right)\end{matrix}\right.\)