cho tam giác ABC có AD ⊥ BC, CK ⊥ AB. Chứng minh ΔACD ~ ΔACK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 9 2019
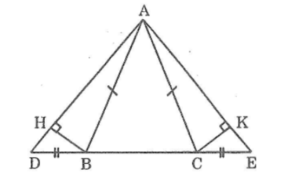
Xét ΔABH và ΔACK, ta có:
AB = AC (gt)
∠(AHB) =∠(AKC) =90o
BH=CK ( chứng minh trên)
Suy ra: ΔABH= ΔACK (cạnh huyền– cạnh góc vuông)
KK
7 tháng 1 2019
A C B D K
CM : Xét tam giác ACD và tam giác ABD
có AC = AD (gt)
góc CAD = góc DAB (gt)
AD : chung
=> tam giác ACD = tam giác ABD (c.g.c)
=> góc CDA = góc BDA (hai góc tương ứng
Mà góc CDA + góc BDA = 1800 (kề bù)
hay 2\(\widehat{BDA}\) = 1800
=> góc BDA = 1800 : 2
=> góc BDA = 900
=> AD vuông góc với BC
b) Ta có : CK \(\perp\)BC => góc C = 900
Ta lại có: góc ADC + góc C = 900 + 900 = 1800
Mà góc ADC và góc C ở vị trí trong cùng phía
=> CK // AD
7 tháng 1 2019
Điểm M nằm trên đường thẳng hay cái gì bạn ? Bạn chỉ nói CM mà không nói vị trí điểm M thì làm sao mà làm ?
21 tháng 12 2015
Đa số những người hỏi câu hỏi về hình học đều muốn mọi người vẽ hình hộ
29 tháng 1 2022
c: Xét ΔCDA có CH là đường phân giác
nên CH/HA=CD/HD
mà CH>CD
nên HA>HD