Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tam giác ACH và tam giác KCH có : CH chung
góc AHC = góc KHC = 90
AH = HK do H là trđ của AK (gt)
=> tam giác ACH = tam giác KCH (2cgv)
b, xét tam giác AEC và tam giác DEB có : góc BED = góc CEA (đối đỉnh)
BE= EC do E là trđ của BC (GT)
AE = ED do E là trđ của AD (gt)
=> tam giác AEC = tam giác DEB (c-g-c)
=> BD = AC (đn)
tam giác ACH = tam giác KCH (câu a) => AC = CK (đn)
=> BD = CK (tcbc)
c, xét tam giác AEH và tam giác KEH có: EH chung
AH = HK (câu a)
góc AHE = góc KHE = 90
=> tam giác AEH = tam giác KEH (2cgv)
=> góc AEH = góc KEH mà EH nằm giữa EA và EK
=> EH là phân giác của góc AEK (đn)

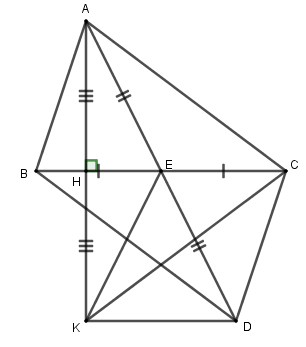
hình bạn nhé :
Xét ΔABEΔABE và ΔDCEΔDCE có :
EB=ECEB=EC (EE là trung điểm BCBC)
EA=EDEA=ED (EE là trung điểm ADAD)
∠AEB=∠DEC∠AEB=∠DEC (đối đỉnh)
⇒ΔABE=ΔDCE(c−g−c)⇒ΔABE=ΔDCE(c−g−c)
b) Chứng minh: AC//BDAC//BD.
Xét ΔACEΔACE và ΔDBEΔDBE có :
EB=ECEB=EC (EE là trung điểm BCBC)
EA=EDEA=ED (EE là trung điểm ADAD)
∠AEC=∠DEB∠AEC=∠DEB (đối đỉnh)
⇒ΔACE=ΔDBE(c−g−c)⇒ΔACE=ΔDBE(c−g−c)
⇒∠ACE=DBE⇒∠ACE=DBE (góc tương ứng)
Mà hai góc ở vị trí so le trong nên AC//BDAC//BD (đpcm)
c) Vẽ AHAH vuông góc với ECEC (HH thuộc BCBC). Trên tia AHAH lấy điểm KK sao cho HH là trung điểm của AKAK. Chứng minh rằng BD=AC=CKBD=AC=CK.
Ta có : ΔACE=ΔDBE(cmt)ΔACE=ΔDBE(cmt)⇒BD=AC⇒BD=AC (cạnh tương ứng) (1)
Xét ΔCAHΔCAH và ΔCKHΔCKH có :
CHCH chung
∠CHA=∠CHK=900∠CHA=∠CHK=900
HA=HK(gt)HA=HK(gt)
⇒ΔCAH=ΔCKH(c−g−c)⇒ΔCAH=ΔCKH(c−g−c)
⇒CA=CK⇒CA=CK (2)
Từ (1) và (2) suy ra AC=BD=CKAC=BD=CK (đpcm)
d) Chứng minh DKDK vuông góc với AHAH.
Nối EE với KK.
Xét ΔEAHΔEAH và ΔEKHΔEKH có :
EHEH chung
∠EHA=∠EHK=900∠EHA=∠EHK=900
HA=HK(gt)HA=HK(gt)
⇒ΔEAH=ΔEKH(c−g−c)⇒ΔEAH=ΔEKH(c−g−c) ⇒∠EAH=∠EKH⇒∠EAH=∠EKH (góc t/ư) (3)
EK=EAEK=EA (cạnh t/ư), mà EA=ED(gt)EA=ED(gt) ⇒EK=ED⇒EK=ED ⇒ΔEKD⇒ΔEKD cân tại EE
⇒∠EKD=∠EDK⇒∠EKD=∠EDK (t/c) (4)
Từ (3) và (4) suy ra ∠EAK+∠EDK=∠EKA+∠EKD=∠AKD∠EAK+∠EDK=∠EKA+∠EKD=∠AKD
Tam giác AKDAKD có : ∠EAK+∠EDK+∠AKD=1800∠EAK+∠EDK+∠AKD=1800
⇒∠AKD+∠AKD=1800⇒2∠AKD=1800⇒∠AKD=1800:2=900⇒∠AKD+∠AKD=1800⇒2∠AKD=1800⇒∠AKD=1800:2=900
Vậy AK⊥KDAK⊥KD (đpcm).
chúc bạn học tốt

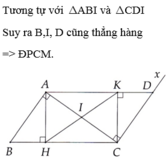
Kiểm tra lại đề nhé!:) D là trung điểm DB ?????