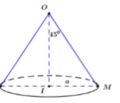
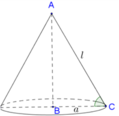
1 Trong không gian, cho tam giác ABC vuông tại A , AC=3a và BC=5a. Khi quay quanh tam giác ABC quanh cạnh góc vuông AB thì đường gấp khúc ACB tạo thành một hình nón. Diện tích xung quanh hình nón đó là
2 cho \(\int_1^3f\left(x\right)dx=4\) . Tính I=\(\int_1^9\frac{f\left(\sqrt{x}\right)}{\sqrt{x}}\) dx là
A.4 B.8 C.2 D.6
3 cho hàm số f(x)= \(\frac{x^2+m^2x-10}{x-1}\) (m là tham số thực) . Tinh tổng các giá trị nguyên của m để hàm số đã cho đồng biến trên khoảng xác định
A .7 B.0 C.6 D.3
4 Cho cấp số nhân (\(u_n\) ) với \(u_2\) =8 và công bội q=3. Số hạng đầu tiên \(u_1\) của cấp số nhân đã cho bằng
5 tìm nghiệm pt \(log_2\left(x-5\right)=3\)
6 Thể tích khối lập phương \(ABCD.A^,B^,C^,D^,\) có AC= \(a\sqrt{6}\) là
7 đạo hàm của hàm số y=\(e^{2x}\)
8 tính \(\int\) \(3^x\)dx, kết quả là
9 khối chóp S.ABC có thể tích V=\(\frac{2\sqrt{2}}{3}\) và diện tích đáy = \(\sqrt{3}\) . Chiều cao của khối chóp S.ABC bằng
10 Bán kính r của khối cầu có thể tích V= \(36\pi\left(cm^3\right)\) là
A r=3(cm) B r= \(\sqrt{27}\)(cm) C r=\(\sqrt[3]{48}\left(cm\right)\) D. r=\(\sqrt[3]{9}\left(cm\right)\)


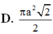


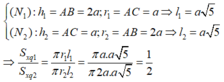

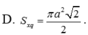



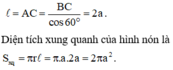
8.
\(\int3^xdx=\frac{3^x}{ln3}+C\)
9.
\(V=\frac{1}{3}S.h\Rightarrow h=\frac{3V}{S}=\frac{2\sqrt{6}}{3}\)
10.
\(V=\frac{4}{3}\pi R^3\Rightarrow R=\sqrt[3]{\frac{3V}{4\pi}}=\sqrt[3]{\frac{3.36\pi}{4\pi}}=\sqrt[3]{27}=3\)
4.
\(u_2=u_1q\Rightarrow u_1=\frac{u_2}{q}=\frac{8}{3}\)
5.
\(log_2\left(x-5\right)=3\Rightarrow x-5=8\Rightarrow x=13\)
6.
\(AC=a\sqrt{6}\Rightarrow AB=\frac{AC}{\sqrt{2}}=a\sqrt{3}\)
\(\Rightarrow V=AB^3=9\sqrt{3}.a^3\)
7.
\(y'=e^{2x}.\left(2x\right)'=2.e^{2x}\)