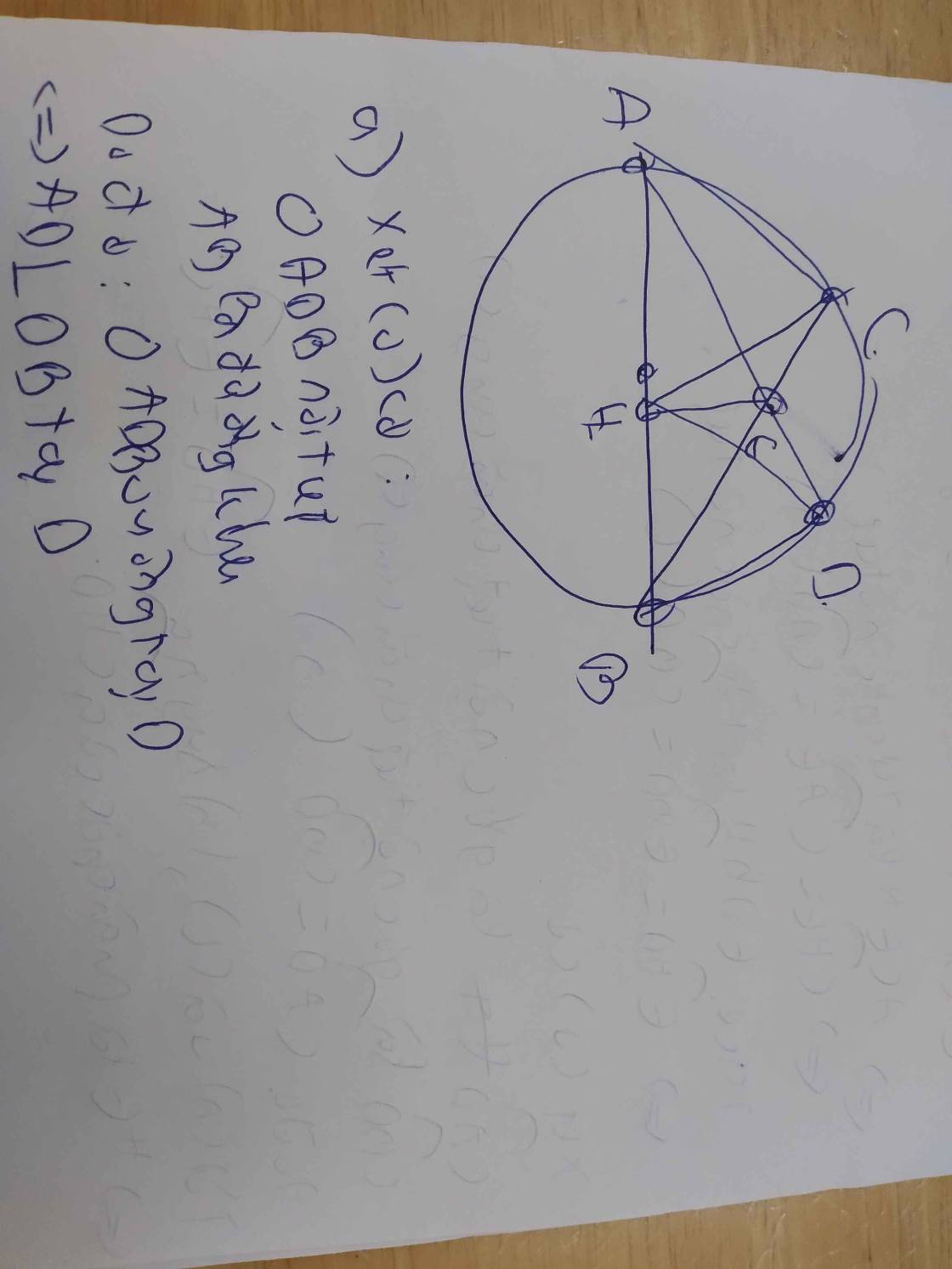
Trên đường tròn (O) có đường kính AB=2R, lấy một điểm C sao cho AC = R và lấy điểm D bất kì trên cung nhỏ BC ( điểm D không trùng với B và C). Gọi E là giao điểm của AD và BC. Đường thẳng đi qua E vuông góc với đường thẳng AB tại H cắt tia AC tại F. Điểm M là trung điểm của đoạn EF
a) Chứng minh tứ giác BHCF nội tiếp
b) Chứng minh HA.HB=HE.HF
c) Chứng minh CM là tiếp tuyến của đường tròn (O)
d) Xác định vị trí của điểm M để tứ giác ABDC có chu vi lớn nhất