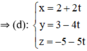Lập pttq của đường thẳng của Δ đi qua 2 điểm: M(-2;1); N(4;0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Phương trình đường thẳng Δ đi qua M(–5; –8) và có hệ số góc k = –3 là:
y = –3.(x + 5) – 8 ⇔ 3x + y + 23 = 0.
b) Ta có: A(2; 1), B(–4; 5) ⇒ 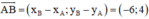
Δ đi qua hai điểm A(2; 1) và B(–4; 5)
⇒ Δ nhận 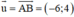 là một vtcp
là một vtcp
⇒ Δ nhận 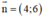 là một vtpt.
là một vtpt.
Phương trình tổng quát của đường thẳng Δ là:
(Δ) : 4(x – 2) + 6(y -1) = 0
Hay 4x + 6y – 14 = 0 ⇔ 2x + 3y – 7 = 0.

1.
Phương trình:
\(2\left(x-3\right)+1\left(y+4\right)=0\Leftrightarrow2x+y-2=0\)
2.
Phương trình tham số: \(\left\{{}\begin{matrix}x=3-3t\\y=-4+3t\end{matrix}\right.\)
3.
\(\overrightarrow{NM}=\left(4;2\right)=2\left(2;1\right)\)
\(\Rightarrow\) Đường thẳng MN nhận (2;1) là 1 vtcp và (1;-2) là 1 vtpt
Phương trình tổng quát (chọn điểm M để viết):
\(1\left(x-3\right)-2\left(y-4\right)=0\Leftrightarrow x-2y+5=0\)
Phương trình tham số: \(\left\{{}\begin{matrix}x=3+2t\\y=4+t\end{matrix}\right.\)

(d): y=ax+b
Vì (d) đi qua điểm I(-1;2) nên: -a+b=2
Mà (d) vuông góc với đth: y=\(\dfrac{2}{3}x+\dfrac{7}{3}\) nên: a.\(\dfrac{2}{3}\)= -1 => a=\(\dfrac{-3}{2}\)
=> b=\(\dfrac{1}{2}\)
Do đó: (d): y=\(\dfrac{-3}{2}\)x+\(\dfrac{1}{2}\)

1: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-2\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=1-2a=1-2\cdot\left(-3\right)=7\end{matrix}\right.\)
2: Vì (d)//y=-3x+2 nên a=-3
Vậy: y=-3x+b
Thay x=3 và y=3 vào y=-3x+b, ta được:
b-9=3
hay b=12

\(A\left(2;0\right);B\left(0;-7\right)\)
\(\Rightarrow\overrightarrow{BA}=\left(2;7\right)\Rightarrow\) đường thẳng AB nhận \(\left(7;-2\right)\) là 1 vtpt
Phương trình AB:
\(7\left(x-2\right)-2\left(y-0\right)=0\Leftrightarrow7x-2y-14=0\)

(Δ) nhận 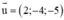 là 1 vtcp
là 1 vtcp
+ (d) cần tìm song song với (Δ)
⇒ (d) nhận 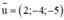 là 1 vtcp
là 1 vtcp
+ (d) đi qua M(2; 3; -5)