Cho tam giác ABC, các đường phân giác BK và CH cắt nhau tại I. Biết góc BIC = 125 độ . tính góc A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2015
BIC=121 độ \(\Rightarrow\)KBC+HCB=180-121=59 độ
MÀ BK là pg góc B; CH là pg góc C \(\Rightarrow\)Góc B + góc C=59.2=118
\(\Rightarrow\)Góc A=180-118=62 độ
Tick mình nha bạn Danh
L
0
HH
3 tháng 5 2018
(Bạn tự vẽ hình giùm)
Ta có \(\widehat{IBC}=\frac{\widehat{ABC}}{2}\)(BD là tia phân giác của \(\widehat{ABC}\))
và \(\widehat{ICB}=\frac{\widehat{ACB}}{2}\)(CE là tia phân giác của \(\widehat{ACB}\))
=> \(\widehat{IBC}+\widehat{ICB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}\)
=> \(180^o-\widehat{BIC}=\frac{180^o-\widehat{A}}{2}\)
=> \(180^o-\widehat{BIC}=90^o-\frac{\widehat{A}}{2}\)
=> \(180^o-90^o=\widehat{BIC}-\frac{\widehat{A}}{2}\)
=> \(\widehat{BIC}-\frac{\widehat{A}}{2}=90^o\)
=> \(\widehat{BIC}=90^o+\frac{\widehat{A}}{2}\)
Thay \(\widehat{A}=80^o\)vào biểu thức \(\widehat{BIC}=90^o+\frac{\widehat{A}}{2}\), ta có:
\(\widehat{BIC}=90^o+\frac{80^o}{2}\)
=> \(\widehat{BIC}=90^o+40^o=130^o\)
22 tháng 5 2021
Ta có ^IBC=^ABC2 (BD là tia phân giác của ^ABC)
và ^ICB=^ACB2 (CE là tia phân giác của ^ACB)
=> ^IBC+^ICB=^ABC+^ACB2
=> 180o−^BIC=180o−^A2
=> 180o−^BIC=90o−^A2
=> 180o−90o=^BIC−^A2
=> ^BIC−^A2 =90o
=> ^BIC=90o+^A2
Thay ^A=80ovào biểu thức ^BIC=90o+^A2 , ta có:
^BIC=90o+80o2
=> ^BIC=90o+40o=130o
2 tháng 7 2023
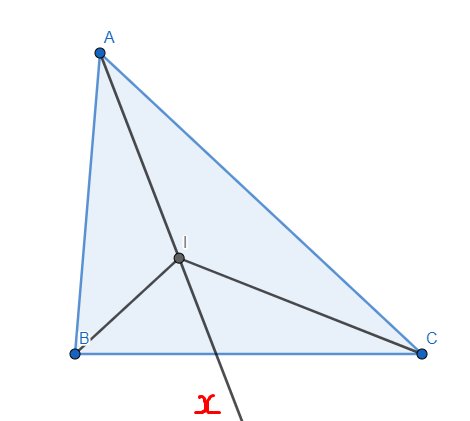
Kẻ tia phân giác Ax của tam giác ABC. Theo tính chất góc ngoài của tam giác, dễ có \(\widehat{BIx}=\widehat{IBA}+\widehat{IAB}\) và \(\widehat{CIx}=\widehat{ICA}+\widehat{IAC}\). Cộng theo vế 2 đẳng thức trên, thu được \(\widehat{BIC}=\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{ACB}}{2}+\widehat{ABC}\) \(=\dfrac{180^o+\widehat{ABC}}{2}\) \(=90^o+\dfrac{\widehat{BAC}}{2}\)
Tới đây mình cũng đã chứng minh xong câu b luôn rồi. Bạn chỉ cần thay số đo góc vào thì tính được câu a.
3 tháng 7 2023
a) (BI và CI lần lượt là các đường phân giác của góc B và C)
Theo đề ta có:
\(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^o\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=180^o-\widehat{BIC}=180^o-140^o=40^o\)
Mà \(\widehat{ABI}=\widehat{CBI}\) và \(\widehat{ACI}=\widehat{BCI}\) (vì BI và CI lần lượt là các đường phân giác của góc B và C)
Suy ra \(\widehat{ABC}+\widehat{ACB}=2\widehat{IBC}+2\widehat{ICB}=2\left(\widehat{IBC}+\widehat{ICB}\right)=2\cdot40^o=80^o\)
Từ đó
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)
\(\Leftrightarrow\widehat{BAC}=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)=180^o-80^o=100^o\)
Ta có \(\Delta BIC=\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^0\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=180^0-\widehat{BIC}=180^0-125^0=55^0\)
Mà \(\widehat{IBC}=\frac{1}{2}\widehat{ABC}\) ; \(\widehat{ICB}=\frac{1}{2}\widehat{ACB}\)
\(\Rightarrow\frac{1}{2}.\widehat{ABC}+\frac{1}{2}\widehat{ACB}=55^0\)
\(\Leftrightarrow\frac{1}{2}.\left(\widehat{ABC}+\widehat{ACB}\right)=55^0\)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=110^0\)
Xét \(\Delta ABC\)có \(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\Leftrightarrow\widehat{A}+110^0=180^0\)
\(\Rightarrow\widehat{A}=70^0\)
Vậy góc A bằng \(70^0\)
Nhớ k cho mình nha