Trong mặt phẳng Oxy, cho đường thẳng \(d_1\) :x-2y+3=0 và hai điểm A(1;3) B(-2;4). Điểm M (x;y) \(\in\) \(d_1\) sao cho \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|\)đạt giá trị nhỏ nhất. Tính giá trị của x+2y
A. 123/25
B. -19/5
C. 19/5
D. 19/10

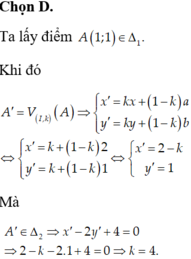
Do M thuộc d nên tọa độ M có dạng: \(M\left(2y-3;y\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(4-2y;3-y\right)\\\overrightarrow{MB}=\left(1-2y;4-y\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}=\left(5-4y;7-2y\right)\)
\(T=\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\sqrt{\left(5-4y\right)^2+\left(7-2y\right)^2}\)
\(T=\sqrt{20y^2-68y+74}=\sqrt{20\left(y-\frac{17}{10}\right)^2+\frac{81}{5}}\ge\sqrt{\frac{81}{5}}\)
Dấu "=" xảy ra khi \(y=\frac{17}{10}\Rightarrow x=\frac{2}{5}\Rightarrow x+2y=\frac{19}{5}\)