ΔABC có 3 cạnh tỉ lệ theo 3 : 4 : 6; gọi M, N, P là trung điểm các cạnh của ΔABC. Tính các cạnh ấy biết rằng chu vi của ΔMNP bằng 5,2m.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 10 2019
Do các cạnh a, b, c tỉ lệ với 3;4;5 nên:
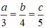
Mà chu vi tam giác ABC bằng 24 cm nên a+ b +c = 24
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
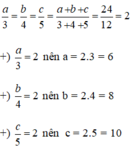
Vậy độ dài ba cạnh của tam giác ABC là 6cm,8cm và 10cm.
CM
18 tháng 6 2018
Vì 
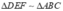nên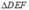 
cũng có độ dài các cạnh tỉ lệ với 4 : 5 : 6.
Giả sử DE < EF < FD Þ DE = 0,8m.
Ta có
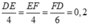
Từ đó tính được EF = 1m và FD = 1,2m
G
25 tháng 9 2017
Theo tính chất đường trung bình của tam giác thì tam giác MNP có các cạnh lần lượt bằng 1/2 các cạnh của tam giác ABC.
=> Chu vi tam giác ABC gấp đôi chu vi tam giác MNP.
Chu vi tam giác ABC là: 5,2 . 2 = 10.4 (m)
Gọi các cạnh của tam giác ABC là: a, b, c thì ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{6}\)
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{6}=\frac{a+b+c}{3+4+6}=\frac{10,4}{13}\)
=> \(a=\frac{10,4}{13}.4=\frac{41,6}{13}\) (m)
\(b=\frac{10,4}{13}.3=\frac{31,2}{13}\) (m)
\(c=\frac{10,4}{13}.6=\frac{122,4}{13}\) (m)
Nếu đề bài hỏi các cạnh tam giác MNP thì lấy các cạnh trên (a ,b, c) chia cho 2.
20 tháng 10 2018
1, Gọi các cạnh của tam giác lần lượt là a,b,c
Ta có : \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\) và \(a+b+c=45\)
Theo tính chất dãy tỉ số bằng nhau, ta có :
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{45}{9}=5\)
\(\Rightarrow\) \(a=10;b=15;c=20\)
31 tháng 12 2019
2, Ta có: f(5)= 2.5=10
3, Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ là 3 thì: y= 3x
4, ... x thì tỉ lệ nghịch với y theo hệ số tỉ lệ là: a
5, .... Ta có: xy= 60 hay x và y tỉ lệ nghịch theo hệ số tỉ lệ là: 60
6, Tọa độ của góc O trong mặt phẳng tọa độ là: (0;0)